Contents:
What is the Ratio Test?
The ratio test tells you whether a series converges (i.e. settles on a certain number) or diverges (does not settle on a certain number). The test is also known as d’Alembert’s ratio test (Jean le Rond d’Alembert is credited with first publishing the test) or as the Cauchy ratio test. It is the main tool for calculating the radius of convergence.
The ratio test is particularly useful for series with factorials (!). You can use the test when:
- Each term is a real number or complex number and
- an is nonzero when n is large.
The ratio test requires that you find a limit, “L”. Once you have found L, you can then figure out whether the series converges or diverges. The ratio test is similar to the limit comparison test but is only used when the series to be compared against equals 1:
- If the ratio is less than 1, the series converges absolutely.
- If the ratio is more than 1 the series diverges.
- If the ratio equals 1, then the series may be divergent, conditionally convergent, or absolutely convergent.
If the ratio equals 1, then the test basically tells you nothing about convergence or divergence. The reason that the test is inconclusive in this case is that even two series with exactly the same successive ratios can have different convergent properties when the limit of the successive ratios are equal to 1. A limit of 1 shows that the terms do not behave as a geometric series in the limit. If you do get a series with a ratio equal to 1, then choose another test for convergence.
Formula
The ratio test is represented algebraically as:
![]()
The formula above tells you to:
- Form a ratio of an + 1/an,
- Take the absolute value of the ratio and the limit as n → ∞.
- Compare L to 1 and determine whether the series converges or diverges.
Ratio Test Examples
Example question: Does the following sequence converge or diverge?
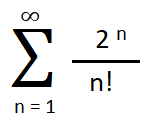
This sequence has a summation symbol(Σ) and a factorial (!). If you aren’t sure what those are, you may want to read about summation notation and factorials first.
Step 1: Form a ratio, following the formula.
![]()
- The denominator (an) is the original sequence (the one given in the question).
- For the numerator (an + 1), you’re adding a “+1” everywhere you see an n.
- Don’t forget to add the absolute value symbol.
If you aren’t sure how to do this, the following graphic shows you the steps:
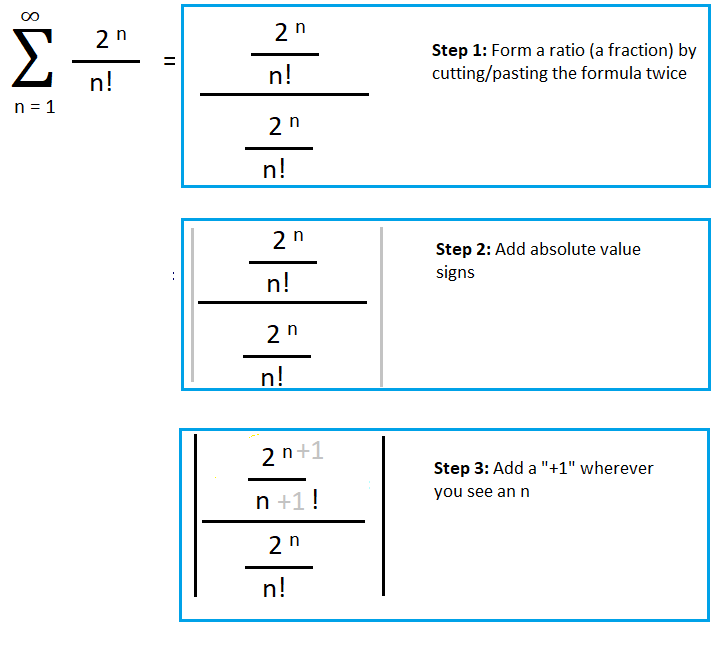
Step 2: Find the limit of Step 1 as n goes to infinity (n → ∞). This is where you might have difficulty, as it does require some strong algebra skills (no calculus needed at this point!). Here are the basic algebraic steps:
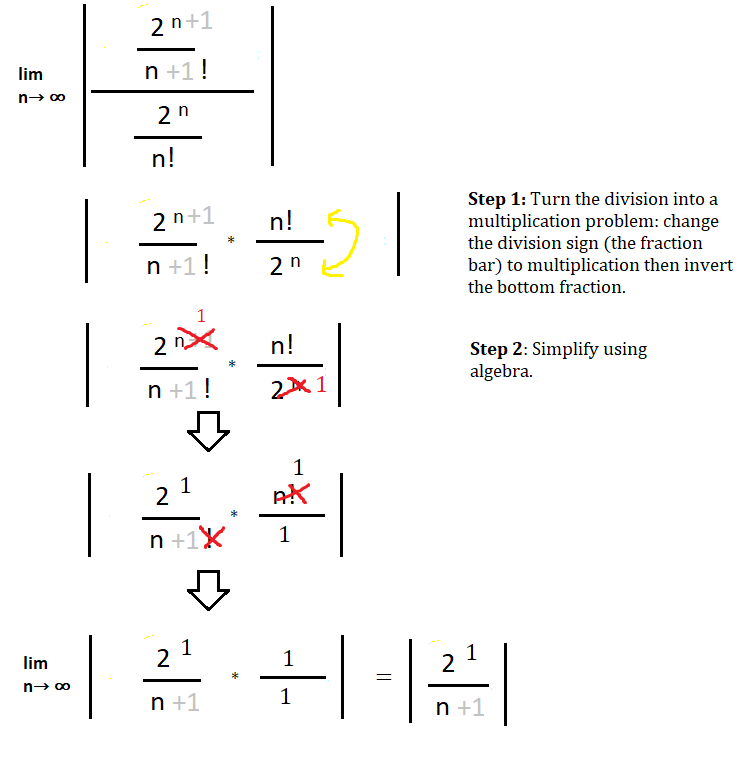
As for the limit, notice that we’re looking for the limit as n goes to infinity. As n gets larger, the denominator is going to get larger. That means it’s going towards 2/∞, which is essentially zero. Therefore, the limit is zero.
Step 3: Compare your answer in Step 2 to 1 and determine whether the series converges or diverges. As the limit is 0, the ratio test rules say that if the ratio is less than 1, the series converges absolutely.
Related Terms
- Rate ratio (epidemiology): compares the incidence of events happening at different times.
- Ratio Scale: a scale of measurement where the difference between values is meaningful, and zero is also meaningful.