A ratio estimator, commonly used in survey sampling, is a ratio of the means of two random variables. They are biased, so corrections for error must be made when using them in experiments.
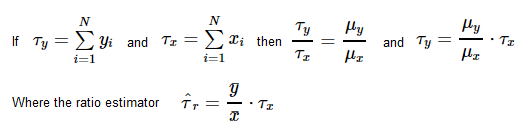
Why Use a Ratio Estimator?
A couple of circumstances could lead you to use a ratio estimator instead of a more simple estimator:
- If y and x are highly linearly correlated through the origin (i.e. x contributes to predicting y),
- If you don’t know the number of elements in the population.
Auxiliary Statistics
Auxiliary statistics can be used to calculate hard to get statistics, with the use of a ratio estimator. An auxiliary variable is an easy to study variable x, used to gather information on the harder-to-research target variable y. For example (Borkowski, n.d.):
| Variable of Interest | Auxiliary |
|---|---|
| Amount of lumber a tree produces | Tree diameter |
| income level of a 50-year-old | number of years of education completed |
| number of farms per county in the US | number of farms per county in the previous census |
Historically, John Graunt (1662) was the first person to use the ratio estimate ratio y/x, for the total population y and registered births (the auxiliary variable x), in the same area for the prior year (Sen, 1993). Laplace used a similar method at a later time to measure the total population of France. There wasn’t a census at the time, so Laplace sampled 30 French communities, getting the following information:
- n = 30
- community population = 2,037,615.
Additional (auxiliary) information that Laplace obtained from government records:
- Total registered births for n = 71,866.33.
Dividing the community population by the actual number of registered births:
- 2,037,615 / 71,866.33 = 28.35.
There was only one registered birth for every 28.35 people. Laplace used this auxiliary information to produce a formula estimating total population in France:
Total population = total number of annual births * 28.35
Cautions
The bias and the variance of a ratio estimator rapidly decrease as the sample size (that they are based on) increases. Therefore, the mean square error for the ratio estimator, or the estimator of a ratio also rapidly decrease.
Sometimes, it’s advantageous to stratify the population before using a ratio estimator (Scheaffer, 2011). However, small sample sizes within strata can lead to problems with bias. This effect can be lessened using a combined ratio estimator (i.e. by using an average estimator across all samples).
References
Borkowski, J. Ratio and Regression Estimation. http://www.math.montana.edu/jobo/st446/documents/ho5a.pdf
Scheaffer, R. et al. (2011). Elementary Survey Sampling. Cengage Learning.
Sen, A. (1993). Some Early Developments in Ratio Estimation. https://doi.org/10.1002/bimj.4710350102