What is the Tukey Test / Honest Significant Difference?
Watch the video for an overview and step by step calculations:
The Tukey Test (or Tukey procedure), also called Tukey’s Honest Significant Difference test, is a post-hoc test based on the studentized range distribution. An ANOVA test can tell you if your results are significant overall, but it won’t tell you exactly where those differences lie. After you have run an ANOVA and found significant results, then you can run Tukey’s HSD to find out which specific groups’s means (compared with each other) are different. The test compares all possible pairs of means.
General Steps
Step 1: Perform the ANOVA test. Assuming your F value is significant, you can run the post hoc test.
Step 2: Choose two means from the ANOVA output. Note the following:
- Means,
- Mean Square Within,
- Number per treatment/group,
- Degrees of freedom Within.
Step 4: Find the critical value in The Q table. For this, you’ll need k, which is the number of groups or treatments and degrees of freedom for the error term.
Step 4: Calculate the HSD statistic for the Tukey test using the formula:
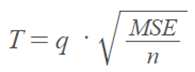
You’ll get MSE from the Anova output (MS error term); “n” is the number of items in one sample.
Step 5: Compare the score you calculated in Step 3 with the tabulated value you found in Step 4. If the calculated value from Step 3 is bigger than the critical value from the Q table, the two means are significantly different.
Assumptions for the test
- Observations are independent within and among groups.
- The groups for each mean in the test are normally distributed.
- There is equal within-group variance across the groups associated with each mean in the test (homogeneity of variance).
Tukey-Kramer Method
If you have unequal sample sizes, you have to calculate the estimated standard deviation for each pairwise comparison. This is called the Tukey-Kramer Method.
References
Brillinger, D. “The Collected Works of John W. Tukey“. 1984.