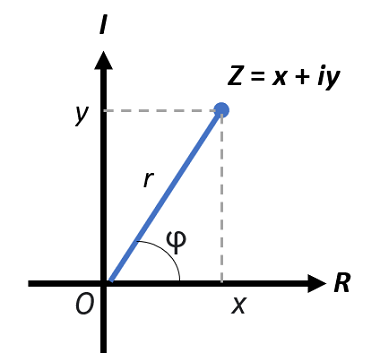
The complex modulus (also called the complex norm or complex absolute value) is the length (i.e., the absolute value) of a complex number in the complex plane. It is usually denoted |z|, but you might also see the notation mod z.
.
How to find the Complex Modulus
Complex modulus is analogous to the absolute value for real numbers, but as complex numbers aren’t ordered, we can’t use the method we would normally use for real numbers. However, as the absolute value of a complex number is simply the (Euclidean) distance from the origin to the number’s position in the complex plane, we can use the Pythagorean theorem to calculate it. As this is a “distance,” the complex modulus is always real and non-negative [1].
Example question: What is the Complex Modulus of z = 1 + 2i?
Solution: |z| = √(12 + 22) = √(5).
Properties of Complex Modulus
- z equals 0 only if |z| = 0.
- In terms of complex conjugation, the modulus can be written as |z| = √(z · z). Geometrically, z is obtained by reflecting z over the real axis. Therefore, the modulus of a complex conjugate z is the same as that of the complex number z.
- If z = a + 0i is real, then |z| = |a| (a complex number z is real if and only if z = z [2]).
- The distance between any two numbers z and w can be calculated by |z – w|.
Disambiguation: Note that the term “complex modulus” has another (unrelated) definition: the ratio of stress to strain under vibratory conditions in materials engineering.
References
[1] Chapter 5: Complex Numbers. Retrieved November 9, 2021 from: http://www2.hawaii.edu/~robertop/Courses/TMP/5_Complex_Numbers.pdf
[2] Sivakumar, N. Chapter 1: Preliminaries.