Finding Area by the Limit Definition
The area of a plane region (i.e., a 2-D shape) between the graph of a function and the x-axis can be found using the limit definition:
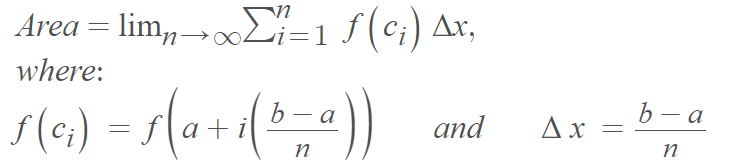
The formula looks complicated, but all you have to do is substitute in your values for the function ( f ) and interval ( b – a ). From there, you can simplify and solve.
Finding Area by the Limit Definition: Example
Example question: Find the area (using the limit definition) between f(x) = 2x3 – x2 and the x-axis, on the interval [1, 2].
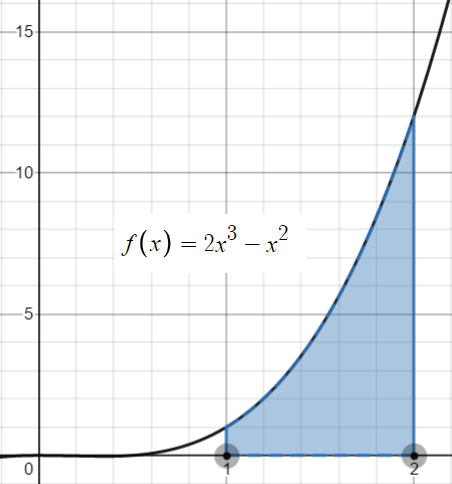
Step 1: (Optional) Make a graph. This not only gives you a visual of what you are trying to find, but you can ballpark your solution to see if your calculated answer makes sense.
Step 2: Find f (ci) by substituting in your interval (a and b) values into the f(ci) formula given above. We are finding the area for the interval between 1 and 2, so substituting those in and simplifying gives us:
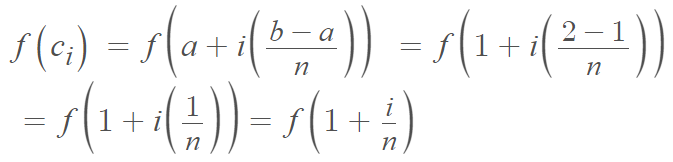
Step 3: Find Δx by substituting your a and b values into the Δx formula from above:
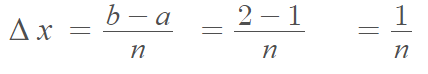
Step 4: Substitute your answers from Step 2 and Step 3 into the main limit definition formula from above:
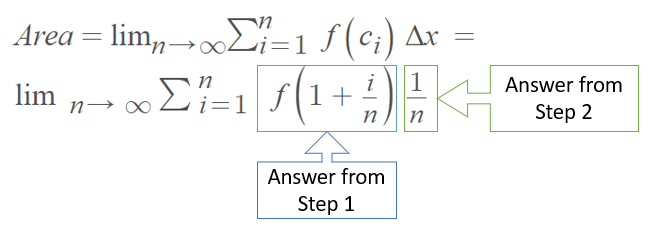
Step 5: Change the generic “f(x)” part of the formula (from Step 4) to your actual function and simplify. Our function for this example is f(x) = 2x3 – x2, so:
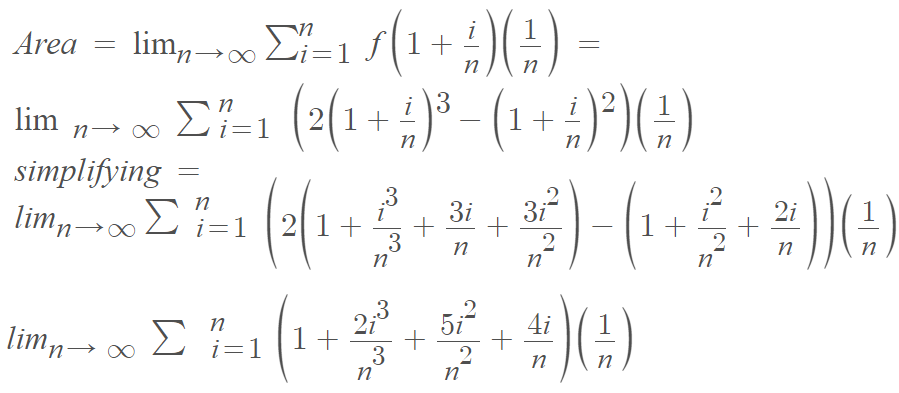
Multiplying (1/n) through each term:
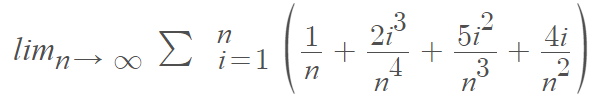
Step 6: Distribute the summation symbol through all terms in your answer from Step 5:
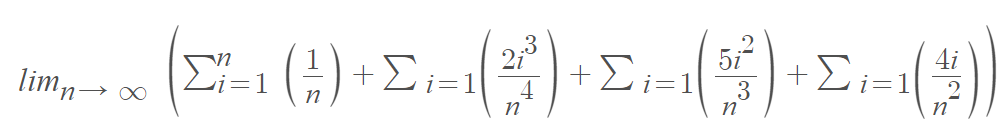
Step 7: Apply summation properties and simplify.
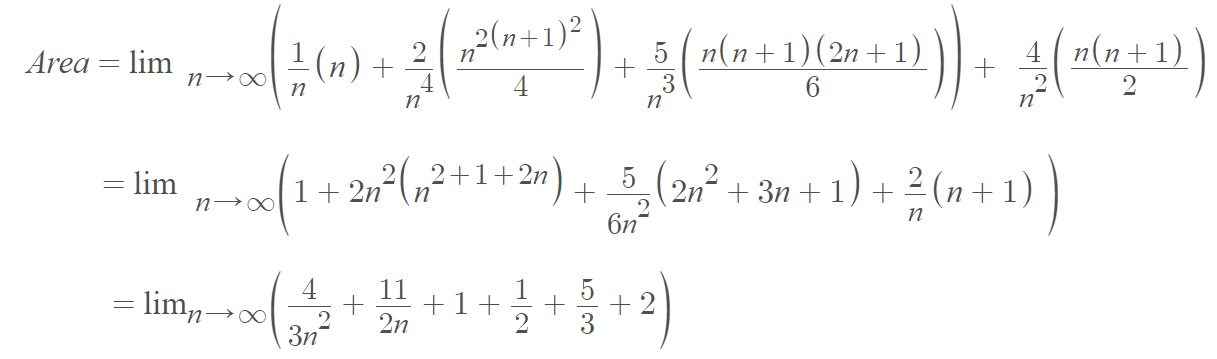
| Term | Summation |
| i3 | |
| i2 | |
| i | |
| c |
Step 8: Find the limit of all the “parts” from Step 7. For this example, we need one property of limits, which is the limit (1/x) = 0 (as x→∞) is 0:
Area = 0 + 0 + 1 + (1/2) + (5/3) + 2 = (31/6).
The solution is 31/6 ≈ 5.167.
References
Graph created with Desmos.com.
Question from Calculus of a Single Variable, 10th edition. 4.2 Exercises, page 264.