 The marginal cost (MC) is the change in total cost when the quantity produced changes by one unit. In other words, it’s the extra cost associate with producing one item.
The marginal cost (MC) is the change in total cost when the quantity produced changes by one unit. In other words, it’s the extra cost associate with producing one item.
More formally, the marginal cost (MC) function is the first derivative of the total cost function with respect to quantity [1].
The MC at k items is the cost of producing one more item. As an algebraic formula, where TC is the total costs, that’s:
MC(k) = TC (k + 1) − TC (k).
The marginal cost units are per item; for example you could say “the marginal cost of one item is $5.”
Sometimes it’s easier to approximate this difference using a calculus formula, using a derivative:
MC(k) = TC′(k).
MC is often used in business, where it’s important to minimize the costs associated with producing extra items. Two important facts to recognize [2]:
- If the average cost is a minimum, then average cost = marginal cost.
- If profit is a maximum, then marginal cost = marginal revenue.
Marginal cost example
If a company’s TC is TC(x) = 0.00002x3 – 0.02x2 + 400x + 50000, what is the marginal cost for the 201st unit?
Step 1: Find the first derivative of the cost function TC(x) = 0.00002x3 – 0.02x2 + 400x + 50000:
I used Symbolab to get:
C′(x) = 0.00006x2 – 0.04x + 400
Step 2: Substitute the given value (200) into the MC function from Step 1:
- C′(200) = 0.00006x2 – 0.04x + 400
- C′(200) = 0.00006x2 – 0.04x + 400
- C′(200) = 2.4 – 8 + 400
- C′(200) = 394.4
The cost of producing the 201st unit is $394.40.
Marginal product and break even point
A marginal product is the additional amount of goods that can be produced by varying one input while holding others constant. For example, you might hold the number of workers constant while varying the number of production lines.
The break even point is where revenue equals costs.
Example question: A photo print has fixed costs of $70 for the printing equipment and marginal costs of 40 cents per copy for ink and labor. If each print sells for 50 cents, what is the break even point?
Step 1: Find the revenue function (RC). The prints sell for $0.50, so the RC is:
R(x) = 0.50x.
Step 2: Find the Cost function. The MC is $0.40 per copy, and the fixed costs are $70 so the cost function is:
C(x) = 0.40x + 70.
Step 3: Graph the two functions.
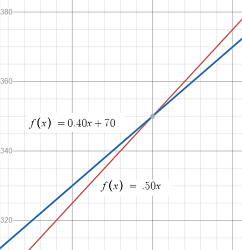
Step 4: Find the Intersection of the two lines.
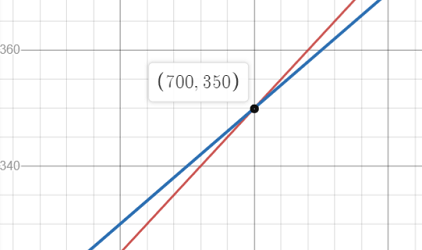
If you have a TI-89 see How to graph two functions and find the intersection on the TI-89..
The coordinates are (700, 350).
Step 5: Identify the “x” value in the coordinates from Step 4. This is the break even point: the “x” units that must be sold to break even.
Break even point = 700 units.
That’s it!
References
[1] Marginal Analysis. Retrieved August 7, 2022 from: https://homepages.math.uic.edu/~rmlowman/math165/LectureNotes/L10-W4L2-165s10-marginalanalysis.pdf
[2] Notes, Lesson 4.7. Applications to Economics.