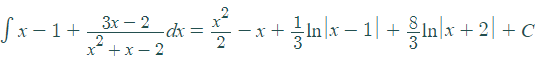Integration Using Long Division works best for rational expressions where the degree of the polynomial in the numerator is greater than or equal to the degree of the polynomial in the denominator.
Integration Using Long Division: Examples
Example question #1: Solve the following integral:
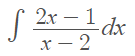
Step 1: Check to see if the degree in the numerator is greater than or equal to the degree in the denominator. For this example, it is, so we can continue.
Step 2: Divide the numerator by the denominator, using algebra:
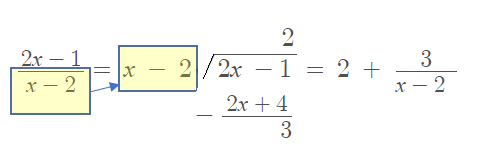
Step 3: Rewrite the integral in the question with the new expression you got in Step 2:
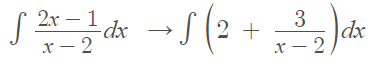
Step 4: Solve the integral using the usual rules of integration:
- Apply the sum rule:
- Apply the common integral ∫1⁄x dx = ln |x| + c: = 2x + 3 ln |x – 2|
- Add a constant: 2x + 3 ln |x – 2| + C
Note: The sum rule states that the integral of the sum of two functions is the sum of their separate integrals:
∫[f(x) + g(x)] dx = ∫f(x)dx + ∫g(x) dx
Example question #2: Solve the following integral:
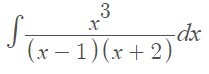
Step 1: Check to see if the degree in the numerator is greater than or equal to the degree in the denominator. For this example, it is, so we can continue.
Step 2: Divide the numerator by the denominator, using algebra:
We can’t actually divide this until we factor the denominator first:
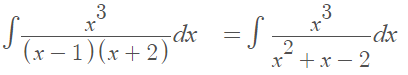
Now we can perform the long division, dividing the numerator by the denominator:
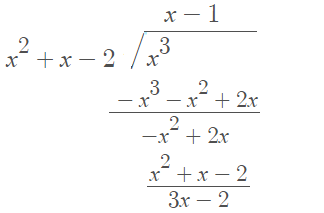
The x – 1 is the quotient and 3x -2 is the remainder. Rewrite the solution above as “quotient + remainder/original factored denominator”:
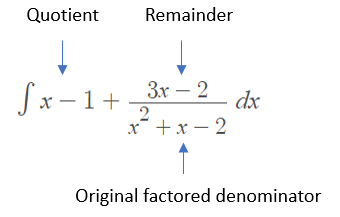
Step 3: Solve the integral using the usual rules of integration: In addition to the sum rule and common integral ∫1⁄x dx = ln |x| + c: = 2x + 3 ln |x – 2|, we also need to apply the power rule to the “x” in front. The solution is: