In general, the implied domain of a function is the set of all real numbers for which the function is defined [1]. If we’re given a function and the domain isn’t specified, we assume that the domain is the largest possible subset of real numbers: (-∞, ∞).
However, there are some notable exceptions [2].
- The radicand of a square root function (the expression contained within the square root) must be zero or greater.
- The denominator in a rational function cannot equal zero.
- Logarithmic functions must have positive real numbers in the domain, because we cannot take the logarithm of negative numbers.
- The radical function
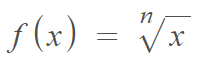
has an implied domain of all reals if n is an even numbered natural number (i.e. the counting numbers 2, 4, 6,….). However, if n is an odd numbered natural number, we can’t take even roots of negative numbers so the implied domain is [0, ∞).
Implied Domain: Examples
Example #1: (Radical Function) Find the implied domain of f(x) = √(x – 2).
Step 1: Set the radicand equal to or greater than zero:
(x – 2) ≥ 0.
Step 2: Solve for x:
x ≥ 2.
This tells us that the implied domain is the set of all real numbers greater than or equal to 2. In interval notation, we can write that as [2, ∞).
Example #2 (Rational Function): Find the implied domain of the following function:
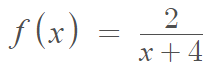
Step 1: Solve the denominator for x.
- x + 4 ≠ 0
- x ≠ -4.
This gives a domain of all real numbers except for -4. In interval notation, the domain is (-∞ -4) ∪ (-4, ∞).
Example #3: (Polynomial Function): What is the implied domain of f(x) = x2 + 5x?
Solution: All polynomial functions have an implied domain of all real numbers. We can write that in interval notation as (-∞, ∞). Or, we can say the domain is ℝ.
A Practical Example
Sometimes you may be asked to find an implied domain for a word problem instead of an algebraic equation. For example, this precalculus worksheet asks you for the implied domain for a function concerning the monthly cost in dollars of a phone call. The input, “x” is the number of minutes used. As there are 43,200 minutes in a month, the longest possible phone call is 43,200 minutes and the shortest call is 0 minutes, giving an implied domain of [0, 43200].
References
[1] Functions. Retrieved October 31, 2021 from: https://people.richland.edu/james/lecture/m116/functions/functions.html
[2] Handout. Retrieved October 31, 2021 from: https://somerset.kctcs.edu/current-students/media/student-support-services/workshops/implied-domain-handout.docx