Interval notation is a shorthand way to show:
- The domain of a function (i.e., where the function is defined [1],
- A range of values that make an inequality true,
- Subsets of the real number line.
Interval Notation Reference List
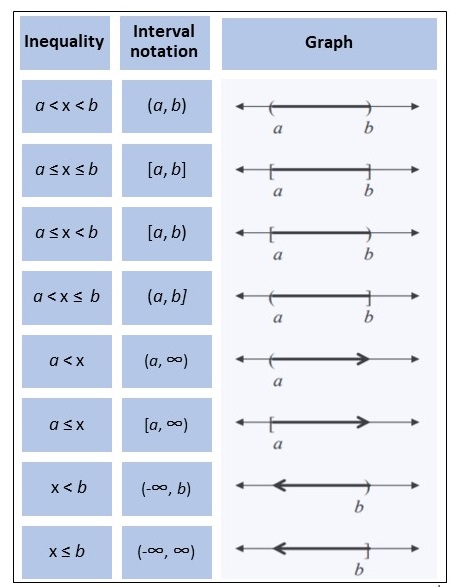
The following image shows representations for inequalities, their respective interval notation, and how they appear on a graph.
The ∞ symbol is used to represent infinity; infinity is not a number, so it should never be paired with a square bracket when using interval notation.
- Positive infinity (∞) indicates there isn’t an endpoint to the right of the number (on the number line).
- Negative infinity (∞) indicates there isn’t an endpoint to the left of the number (on the number line).
Note that on a graph, a closed circle ● can be used instead of brackets [ ] and an open circle ○ can be used instead of parentheses ( ). 1
Some General Tips
The smaller value of the interval goes first and the larger value of the interval goes second; the two values are separated by a comma. Parentheses indicate an open interval and square brackets a closed interval, although you can also have a mixture of the two, giving a half closed or half open interval. For example:
- (2, 9) = an open interval from 2 to 9 (does not include 2 and 9 as endpoints).
- [2, 9] = a closed interval from 2 to 9 (includes 2 and 9 as endpoints).
- [2, 9) = a half-closed interval from 2 to 9 (includes 2 as an endpoint, but not 9).
Not sure what closed, open, and half-closed intervals are? Watch the video for an overview:
If you have either infinity or negative infinity on either end of the interval, you always use a curve for that end. This will indicate that there is no definite endpoint in that direction, it keeps going and going.
References
[1] Domain and Range.
[2] Interval Notation. Retrieved November 4, 2021 from: https://math.osu.edu/sites/math.osu.edu/files/1148-interval-notations.pdf