ANOVA > Huynh-Feldt Correction
The Huynh-Feldt correction is a correction for violations of sphericity.
If Mauchly’s Sphericity Test test returns a small p-value, you should apply a correction to the index of non sphericity (called the Box index, ε):
- When ε ≤ 0.75 (or you don’t know what the value for the statistic is), use the Greenhouse-Geisser correction. This is a conservative correction that increases the risk of Type II error.
- When ε > 0.75, use the Huynh-Feldt correction. Abdi (2010) describes this correction as more efficient, and more powerful than the Greenhouse-Geisser correction.
There is some debate about which correction is “best”. Abdi (2010) states that, of the two, the Huynh-Feldt is preferred because the Greenhouse-Geisser is too conservative. However, the HF correction is regarded by some as too liberal, overestimating sphericity (e.g. Maxwell & Delaney, 1990).
Huynh-Feldt correction Formula
The formula for the Huynh-Feldt correction (from Abdi, 2010) is:
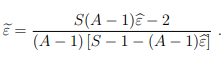
Where:
- S = Number of subjects,
- A = Number of treatments,
= Estimate for ε.
References
Abdi, H. The Greenhouse-Geisser Correction. In Neil Salkind (Ed.), Encyclopedia of Research Design.
Thousand Oaks, CA: Sage. 2010. Retrieved July 1, 2019 from: https://www.utdallas.edu/~herve/abdi-GreenhouseGeisser2010-pretty.pdf
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Greenhouse, S.W., & Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24, 95–112
Huynh, H., & Feldt, L.S. (1976) Estimation of the Box correction for degrees of freedom from
sample data in randomized block and split-plot designs. Journal of Educational Statistics,
1, 69–82
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Maxwell, S.E. & Delaney, H.D. (1990). Designing experiments and analyzing data: A model comparison perspective. Belmont: Wadsworth.