Unidimensionality > Guttman Scale
What is the Guttman Scale?
In the social sciences, the Guttman or “cumulative” scale measures how much of a positive or negative attitude a person has towards a particular topic.
The Guttman scale is one of the three major types of unidimensional measurement scales. The other two are the Likert Scale and the Thurstone Scale. A unidimensional measurement scale has only one (“uni”) dimension. In other words, it can be represented by a number range, like 0 to 100 lbs or “Depressed from a scale of 1 to 10”. By giving the test, a numerical value can be placed on a topic or factor.
The scale has YES/NO answers to a set of questions that increase in specificity. The idea is that a person will get to a certain point and then stop. For example, on a 5-point quiz, if a person gets to question 3 and then stops, it implies they do not agree with questions 4 and 5. If one person stops at 3, another at 1, and another at 5, the three people can be ranked along a continuum.
Examples
The scale is designed to measure one factor or subject. For example, the following shows a questionnaire for a person’s attitudes towards depression:

Sometimes, sensitive topics are concealed within other questions to disguise the intent of the questionnaire. For example, this one quizzes for possible gaming addiction:

One disadvantage of the Guttman scale is that respondents may feel overly committed to questions; They may continue to answer YES beyond the point where they should have stopped. Using the concealed questionnaire helps to avoid this issue.
Use in Education
In the social sciences, the Guttman scale is often used to measure an increasing amount of “attitude” towards a single topic. In education, it’s sometimes used to show a student’s logical progression through coursework. For example, the expected progression through math topics for 3 children. It’s expected that a child does well in fractions before they are able to grasp algebra. A “0” means that the student hasn’t mastered a topic, while a “1” means that a student has mastered it:
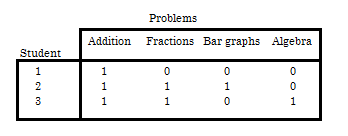
In practice, it’s rare to find data that fits perfectly to a Guttman scale. More often than not, you’re actually testing more than one factor. For example, algebra may need good reading skills as well as the ability to solve an equation. If you know (or suspect) that your instrument is measuring two or more factors, use multidimensional scaling or Correspondence Analysis to analyze your results.