Curves or surfaces with intrinsic coordinates do not depend on a particular coordinate system; they can be measured intrinsically — within the curve or surface itself — without referencing a larger space [1].
Intrinsic coordinates have been around since the early 19th century. However, the system isn’t very versatile and so isn’t widely used. Other names for the system include convected, curvilinear, local, and natural coordinates [2].
Example of Intrinsic Coordinates
For example, in the Cartesian coordinate system, a point on a curve can be described by a location (x, y). In an intrinsic coordinate system, the point might be described by its position relative to the length of an arc s and an angle ψ which the tangent line at the point makes with the x-axis [3].
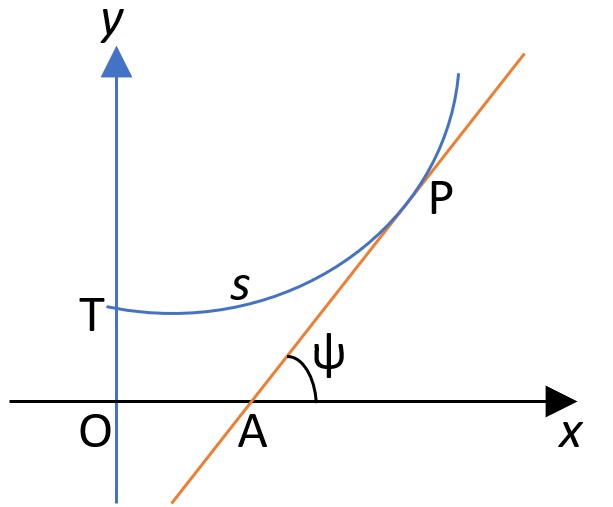
A curve that has the equation s = f(ψ) is said to be given intrinsically [4].
Where are Intrinsic Coordinates Used?
Intrinsic coordinates are used in coordinate free geometry, where geometric objects and relations can be expressed without reference to a particular coordinate system [5]. In practice, it’s usually not very useful to convert Cartesian or polar equations for curves to intrinsic coordinates as those systems are much more versatile. For example, a point (i.e., a location in space) has no intrinsic properties. Therefore, it isn’t possible to represent a general point in the plane using intrinsic coordinates; you can only represent a point on a curve [6].
References
[1] Intrinsic Geometry. Retrieved January 29, 2022 from: https://math.etsu.edu/multicalc/prealpha/Chap3/Chap3-8/printversion.pdf
[2] Mathematical Modeling and Optimization of Complex Structures (2015). Springer International Publishing.
[3] Gaulter, B. & Gaulter, M. (2001). Further Pure Mathematics. OUP Oxford.
[4] Horadam, A. (2014). Outline Course of Pure Mathematics. Elsevier Science.
[5] Coordinate Free Geometry. Retrieved January 29, 2022 from: http://www.dgp.toronto.edu/~karan/courses/418/notes/Coordfreegeom.pdf
[6] Evans, C. (2019). Engineering Mathematics. A Programmed Approach, 3rd Edition. CRC Press.