End Behavior, Local Behavior (Function)

Calculus Definitions >

Contents:

1. End Behavior of a Function
2. Local Behavior of a Function
   • Finding Turning Points and Intercepts

1. End Behavior of a Function

The end behavior of a function tells us what happens at the tails; where the independent variable (i.e. “x”) goes to negative and positive infinity.

There are three main types of end behavior:

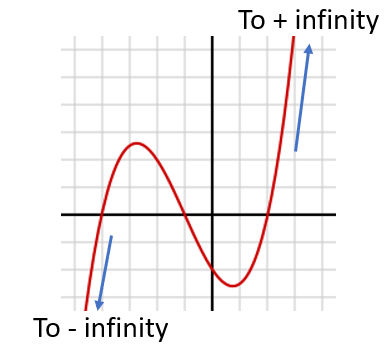
• Infinite: limit of the function goes to infinity (either positive or negative) as x goes to infinity. In other words, what happens as the graph of a function moves to the left, or to the right. The function below, a third degree polynomial, has infinite end behavior, as do all polynomials:
  
  
• Finite: The limit of the function goes to some finite number as x goes to infinity. For example, the function f(x) = 5x / (x² – 4) tends to zero at both ends:
  
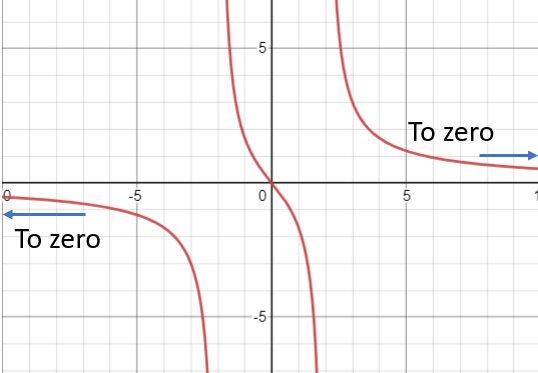
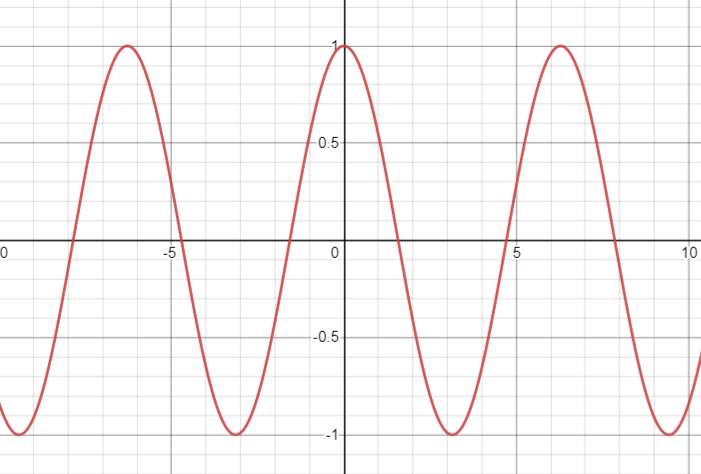
  In fact, any rational function where the degree of the numerator is smaller than the degree in the denominator will always have a horizontal asymptote at zero.
• There are also cases where the limit of the function as x goes to infinity does not exist; these are typically oscillating functions like the sine function. The graph of f(x) = cos(x) has oscillating behavior at the ends (it never settles on a limit):
  
  

End Behavior of a Polynomial

Though a polynomial typically has infinite end behavior, a look at the polynomial can tell you what kind of infinite end behavior it has. There are two important markers of end behavior: degree and leading coefficient.

• The degree is the additive value of the exponents for each individual term. To find the degree:
  1. Add up the values for the exponents for each individual term.
  2. Choose the sum with the highest degree.
• The leading coefficient is the number in front of the variable with the largest exponent.

The end behavior, according to the above two markers:

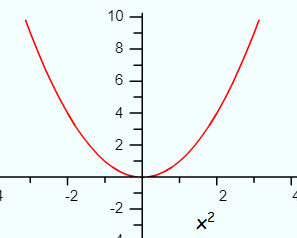
• If the degree is even and the leading coefficient is positive, the function will go to positive infinity as x goes to either positive or negative infinity. We write this as f(x) → +∞, as x → −∞ and f(x) → +∞, as x → +∞.

  A simple example of a function like this is f(x) = x². The graph of this function is a simple upward pointing parabola





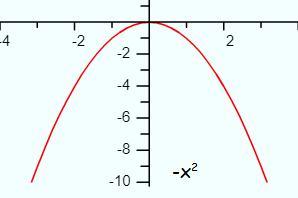
• If the degree is even and the leading coefficient is negative, the function will go to negative infinity as x goes to either positive or negative infinity. We write this as f(x) → −∞, as x → −∞ and f(x) →−∞, as x → +∞.

  An example of this type of function would be f(x) = -x²; the graph of this function is a downward pointing parabola.




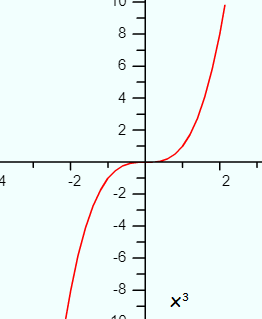
• If the degree is odd and the leading coefficient is positive, the function will go to positive infinity as x goes to positive infinity, and negative infinity as x goes to negative infinity. We write this as f(x) → +∞, as x→ +∞ and f(x) → −∞, as x→ −∞.

  An example of this is f(x) = x³




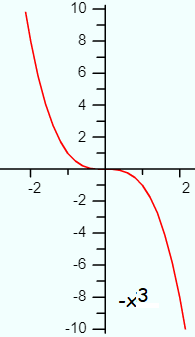
• If the degree is odd and the leading coefficient is negative, the function will go to negative infinity as x goes to positive infinity, and negative infinity as x goes to positive infinity. We write this as f(x) → +∞, as x→−∞ and f(x) → −∞, as x → +∞.

  An example of this is f(x) = -x³.

2. Local Behavior

In addition to end behavior, where we are interested in what happens at the tail end of function, we are also interested in local behavior, or what occurs in the middle of a function. 

The point is to find locations where the behavior of a graph changes.  These turning points are places where the function values switch directions. For example, a function might change from increasing to decreasing.

On the graph below there are three inflection (turning) points labeled a, b and c:

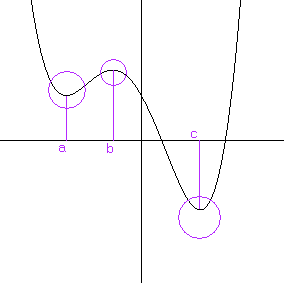
You would typically look at local behavior when working with polynomial functions. 

3. Example—Local Behavior and Finding the Number of Turning Points and Intercepts

Once you know the degree, you can find the number of turning points by subtracting 1.  So, where the degree is equal to N, the number of turning points can be found using N-1.

Example question: How many turning points and intercepts does the graph of the following polynomial function have?
f(x) = x³ – 4x² + x + 1

Step 1: Find the number of degrees of the polynomial.
The degree in the above example is 3, since it is the highest exponent.  Therefore, the function will have 3 x-intercepts. 
Step 2: Subtract one from the degree you found in Step 1:
N – 1 = 3 – 1 = 2. 
This function has two turning points.

References

Rational Functions. Retrieved July 13, 2021 from: https://wwwi.scottsdalecc.edu/softchalk/math/rational_functions/rational_functions_print.html
Math 175 5-1a Notes and Learning Goals
Retrieved from https://math.boisestate.edu/~jaimos/classes/m175-45-summer2014/notes/notes5-1a.pdf on October 15, 2018.
Wilson, J. Introduction to End Behavior. EMAT 6680. Retrieved from http://jwilson.coe.uga.edu/EMAT6680Fa06/Fox/Instructional%20Unit%20Folder/Introduction%20to%20End%20Behavior.htm on October 15, 2018.