Constant Sequence, Eventually Constant

Sequence and series >

A sequence where all the terms are the same real number is a constant sequence. For example, the sequence {4} = (4, 4, 4, …) is a constant sequence.

More formally, we can write a constant sequence as a_n = c for all n, where a_n are the terms of the series and c is the constant. The terms of the sequence {5} could be written as:

• a₁ = 5
• a₂ = 5
• a₃ = 5
• a₄ = 5
• a_n = 5

The constant sequence is a special case of the eventually constant sequence, where a natural number N exists, so that if n ≥ N then a_n = a_N. In other words, somewhere along the line, the sequence will converge on a natural number. For example, the sequence {1, 2, 3, 4, 4, 4, 4, 4, …} is eventually constant.

Constant Sequence Rule

The constant sequence rule states that the limit of an infinite constant sequence with value “c” is also “c”. More formally, we can write that as [1]:

If a sequence is defined by


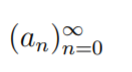
with constant value “c”, then:

Constant Sequence Convergence

All constant sequences converge to the real-numbered term in the sequence ^[2]. For example, the sequence (2, 2, 2, …) converges to 2.

The proof for convergence of a constant sequence is fairly straightforward and short, because you’re only dealing with a single constant, c.

Suppose that a_n = c for all n ∈ ℕ. To prove the limit for the sequence, as n → ∞, is c, you need to show that, given any ε > 0, there
is a natural number (n N ∈ ℕ) where n ≥ N implies |a_n − c| < ε.

We know that a_n = c for n ∈ ℕ, so we have |a_n – c| = 0 for all n ∈ ℕ. This means that the statement above (n ≥ N implies |a_n − c| < ε) holds for all ε > 0 and all n ∈ ℕ^[3].

References

[1] Math 8 Winter 2020 Taylor Polynomials and Taylor Series Day 2. Retrieved April 3, 2021 from: https://math.dartmouth.edu/~m8w20/lectures/m8w20notes2.pdf
[2] 6.4. Properties of Limits. Retrieved April 4, 2021 from: http://people.reed.edu/~mayer/math111.html/header/node34.html
[3] Hildebrand, A. Math 347 Worksheet: Epsilonics, I: Sequences and Limits —SOLUTIONS. Retrieved April 4, 2021 from: https://faculty.math.illinois.edu/~hildebr/347.summer19/epsilonics1sol.pdf