What is “Continued Sum”?
Continued sum is an informal term that can mean one of several things in mathematics.
1. Sigma Notation
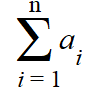In calculus, continued sum usually refers to Sigma (summation) notation. Summation notation involves adding up every point in a set of data—a continuation of summing, or summing up over and over again [1].
2. Integration
Continued sum might also refer to integration and the integral sign ( ∫ ). That’s because integration involves —like it’s cousin, sigma notation — adding up again and again. The difference between sigma notation though, is that with integrals you’re adding up infinitely many tiny pieces; summation notation usually involves finite (fixed) amounts, or at least, very well defined amounts.
Leibniz popularized a “∫” as notation of the continued sum to find the area under a curve.
3. Continued Sum of a Series
Sometimes the term might just refer to something a little simpler than integration or sigma. Outside of calculus (for example, in elementary algebra), you might see this definition, which means “a sum that goes on—and on.”
This is usually in relation to a series (a list of ordered numbers that are added).
For example, let’s say you had a series defined by:
X1 + X2 + …Xn—
This indicates an infinite series, one that goes on, and on, until infinity.
The sum of the first terms in the series might be 1 + 2 + 3 = 6. But as this is an “infinite series“, we could continue the sum for as far as we want: 1 + 2 + 3 + 4 + 6….
References
[1] Barrow, D. (1936). Infinite Exponentials. Retrieved April 22, 2020 from:https://www.math.usm.edu/lee/BarrowInfiniteExponentials.pdf