The constant rule of integration tells you how to find an integral for a constant quantity like 7, ⅓ or π. The rule is defined as:
∫a dx = ax.
Constant Rule of Integration Examples
Example problem #1: Use the constant rule of integration to evaluate the indefinite integral y = ∫ 4 dx.
Step 1: Place the constant in the question into the rule:
∫4 dx → 4x.
Step 2: Add a “+ C” (Why add a + C”?):
The solution is 4x + C.
Example problem #2: Evaluate the indefinite integral ∫ ½ dx.
Step 1: Place the constant into the rule:
½ dx → ½.
Step 2: Add a “+ C”:
The solution is ½x + C.
Example problem #3: Evaluate the following:
![]()
Step 1: Place the constant into the rule:
= (6/π)x.
Step 2: Add a “+ C”:
The solution is = (6/π)x + C.
Notice that in the above problem π is a constant, so you can use the constant rule of integration. Euler’s number e is also a constant, so you can use this rule. However, ex is not a constant because of the x. However, the integral of ex is itself: ex + C.
Constant Multiple Rule
The constant multiple rule for integrals is similar, but this time we’re concerned with finding an integral for a function multiplied by a constant:
The integral of ∫c f(x) dx is c ∫f(x) dx.
They are almost exactly the same: the constant is brought out in front of the integral. In the case of the constant rule of integration though, that process only leaves “dx”, which is converted to x in our integral. With the constant multiple rule there is still a function f(x) to evaluate after you’ve used the constant multiple rule.
Example problem #4: Evaluate ∫5x dx.
Step 1: Pull the constant out in front:
5 ∫x dx.
Step 2: Integrate x with the power rule and simplify:
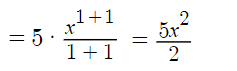
Step 3: Add a + C:
![]()