The Completing the square method is one way to solve a quadratic equation. It requires a few more steps than some of the other methods (like the quadratic formula), but it forms a foundation for an integration method of the same name.
Contents:
Completing the Square Method: Solving Quadratic Equations
Example question: Solve 2x2 + 12x – 18 = 0 by completing the square.
Step 1: Separate the constant term from the other terms by moving it to the right side of the equation. Adding 18 to both sides gives:
2x2 + 12x = 18.
Step 2: Remove any coefficient from x2. For this example, we can get rid of the “2” by dividing:
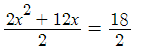
This gives x2 + 6x = 9.
Step 3: Halve the x-coefficient, square it, then add the result to both sides. The x-coefficient is 6, so:
- Halving the x-coefficient: ½ * 6 = 3
- Squaring: 32 = 9
- Adding to both sides: x2 + 6x + 9 = 18.
Step 4: Factor the left side of the equation from Step 3:
Factoring x2 + 6x + 9:
- (x + 3(x + 3) = 18
- (x + 3)2 = 18
I skipped a few factoring steps here, but if you’re a bit rusty, you can view the intermediate steps on Symbolab.
Step 5: Solve for x:
- Take the square root of both sides:
- √[(x + 3)2] = ±√(18)
- x + 3 = ±√18
- Subtract 3 from both sides: x = ±√18 – 3
The solution is x = ±√18 – 3, which simplifies to x = -3±3√2.
Integration of Fractions
The Completing the Square Method is a method of last resort to deal with expressions that can’t be integrated using the “usual” rules like the power rule. Specifically, you use this method when you have a quadratic polynomial in the denominator and no variables in the numerator.
Example question: Find the integral by completing the square:
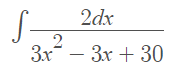
Step 1: Bring the constant in front and rewrite with dx at the end:
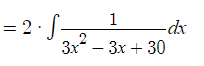
Step 2: Complete the square for the denominator only (following the above procedure for quadratic equations):
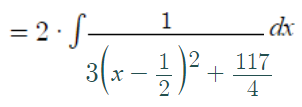
That’s it! Now the function is in a form where you can use the usual rules of integration. For this particular function, you can solve it with u-substitution:
 Substitute u = x – 1
Substitute u = x – 1  Integral Substitution u = 3√3 / √3 v
Integral Substitution u = 3√3 / √3 v
 Take out the constant
Take out the constant Use the common integral ∫ 1/(v2 + 1) dv = arctan (v)
Use the common integral ∫ 1/(v2 + 1) dv = arctan (v) Substitute the original function back in and simplify
Substitute the original function back in and simplify
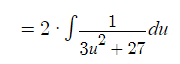 Substitute u = x – 1
Substitute u = x – 1 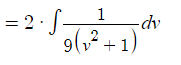 Integral Substitution u = 3√3 / √3 v
Integral Substitution u = 3√3 / √3 v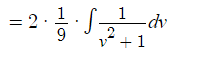 Take out the constant
Take out the constant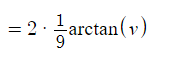 Use the common integral ∫ 1/(v2 + 1) dv = arctan (v)
Use the common integral ∫ 1/(v2 + 1) dv = arctan (v)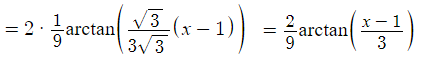 Substitute the original function back in and simplify
Substitute the original function back in and simplify
Hi. I am pretty sure that your example is worked incorrectly. When you complete the square for 3x^2 -3x+30, you would end up with (x-1/2)^2 rather than (x-1)^2.
You’re right! I made the correction. Thanks for catching that :)