Bolzano’s Theorem (Intermediate Zero Theorem)

Calculus Definitions >

Simply put, Bolzano’s theorem (sometimes called the intermediate zero theorem) states that continuous functions have zeros if their extreme values are opposite signs (- + or + -). For example, every odd-degree polynomial has a zero.

Bolzano’s theorem is sometimes called the Intermediate Value Theorem (IVT), but as it is a particular case of the IVT it should more correctly Bolzano’s Intermediate Value theorem.

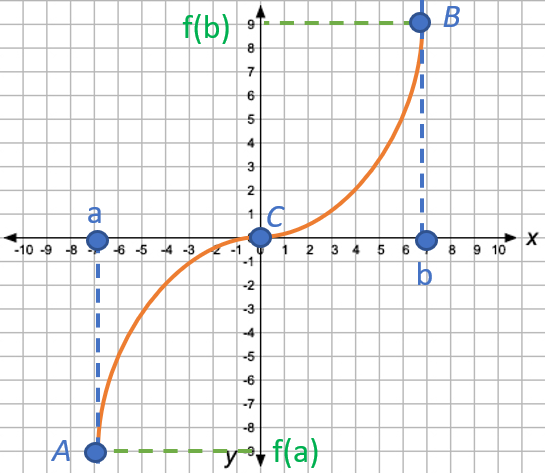
Bolzano’s Theorem: Formal Definition

More formally, Bolzano’s theorem can be stated as follows:

If a function f on the closed interval [a, b] ⊂ ℝ → ℝ is a continuous function and it holds that f(a) f(b) < 0, then there is at least one x ∈ (a, b) such that f(x) = 0

If you’re unfamiliar with the notation:

• ⊂ = proper subset,
• ∈ = “is in” (i.e. “is an element of some set”).
• ℝ = The set of real numbers

Given a function, you can use the theorem to prove that the function has at least one root. The theorem states nothing about what the value for the function’s zero will be: it merely states that the zero exists.

Example

Example question: Does the equation x³ + x – 1 = 0 have at least on real solution in the closed interval [0, 1]?

Here, you’ve been given a function (x³ + x – 1) set to zero. So if the function has at least one solution, then that solution is a root (i.e. a zero). In order to apply Bolzano’s theorem, you need to find out two things:

1. Is the function is a continuous function?
2. Do the interval endpoints have opposite signs?

Step 1: Verify that the function is a continuous function. x³ + x – 1 is a polynomial function, so it meets this requirement.

Note: you may want to read this article about checking continuity if you’re unsure about when functions are continuous (or when they are not).

Step 2: Locate the endpoints and see if they have opposite signs. Here, you’re given the function and the endpoints [0, 1], so plug the endpoints into the function and see what values come out:

• 0³ + 0 – 1 = -1
• 1³ + 1 – 1 = 1

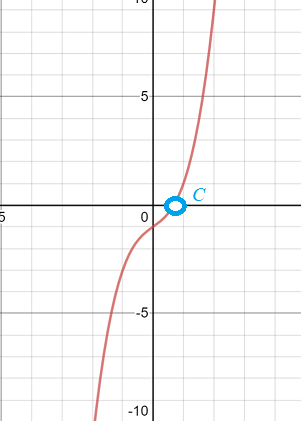
The two values have opposite signs, and the function is continuous. Therefore, Bolzano’s theorem tells us that the equation does indeed have a real solution. A quick look at the graph of x³ + x – 1 can verify our finding:

References

Apostol, T. M. Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, p. 143, 1967.
Rusnock, P. Bolzano’s philosophy and the emergence of modern mathematics. Rodopi. 2000.

Graph paper image from: Free Printable Graph Paper.