Contents:
Definition of the Squeeze Theorem
Formal Definition
Find a limit: Example
What is the Squeeze Theorem?
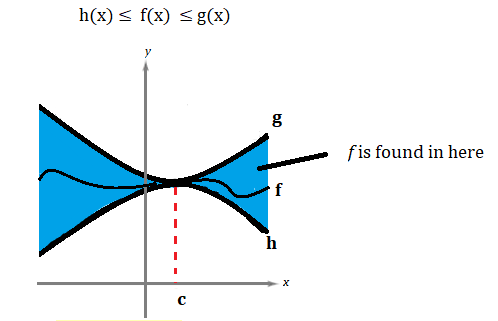
The squeeze theorem (also called the sandwich theorem or pinching theorem), is a way to find the limit of one function if we know the limits of two functions it is “sandwiched” between. It can be a little challenging to find the functions to use as a “sandwich”, so it’s usually used after all other options like properties of limits and graphing (see: Limits involving infinity) have been exhausted.
In some languages it’s called the two policeman theorem, because if two policeman, with a drunken prisoner handcuffed between them, are headed to a jail cell, the prisoner will get there too—no matter how much he wobbles or totters along the way.
Example
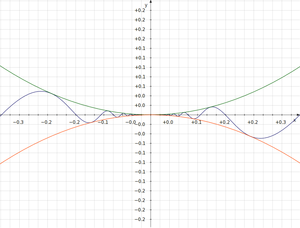
The above graph shows three functions:
- y = x2,
- y = -x2, and
- y = x2sin(1/x).
The limit of the first two functions go to 0 as x goes to 0. Since y = x2sin(1/x) is sandwiched between them, the limit of y = x2sin(1/x) will also be zero. The usefulness of the squeeze theorem is that finding limits of simple functions like x2 is much simpler than finding the limit for a function that wavers everywhere (for example, you can use direct substitution to find limits for simple functions).
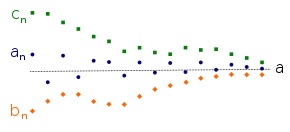
This theorem is valid for sequences as well as for functions, as you can see in the image below.
Formal Statement of the Sandwich Theorem
The sandwich theorem can be stated formally (from Larsen & Edwards, 2008) as:
If h(x) ≤ f(x) ≤ (gx) for all x in open interval containing c, except possibly at c itself, and if
![]()
then ![]() exists and is equal to L.
exists and is equal to L.
The functions g and h we call the lower bound and upper bound of f; the are equivalent to the two slices of bread in a sandwich, or the two policemen conveying the prisoner to jail.
Squeeze Theorem Example
Warning: The idea of the squeeze theorem is fairly intuitive, especially if you’re comfortable by graphs. However, you’ll need some fairly strong algebra skills to actually use the theorem.
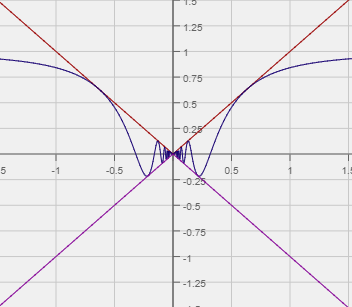
The limit of the function y = x sin (1/x) doesn’t exist, but we do know that the sine function in general falls between 1 and -1. Therefore, if we want to estimate the limit, we know it’s going to be somewhere between -1 and 1. Looking at the graph, you can hazard a guess that the limit is 0, but you can make that more concrete with a little math.
The sine function in general falls between 1 and -1, so we know that:
|x sin(1/x)| ≤ 1 (for all x ≠ 0).
Multiplying by |x|, we get:
|x sin(1/x)| ≤ |x|
From there, we get (use the graph to help visualize this step):
– |x| ≤ x sin(1/x) ≤ |x|
The limit of – |x| and |x| at x = 0 are both zero, so you can conclude that the limit of x sin(1/x) at x = 0 is also zero.
References
Kouba, Duane. “Limits of Functions Using the Squeeze Principle.” http://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/squeezedirectory/SqueezePrinciple.html
Larson, R. & Edwards, B. (2008). Calculus of a Single Variable. Cengage Learning.
MIT World Web Math: The Squeeze Theorem. Retrieved from http://web.mit.edu/wwmath/calculus/limits/squeeze.html on January 20, 2019.
Rogawski, J. Single Variable Calculus: Early Transcendentals.