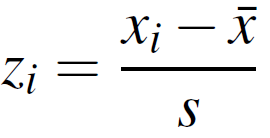Statistics Definitions > Continuity Correction Factor
What is the Continuity Correction Factor?
A continuity correction factor is used when you use a continuous probability distribution to approximate a discrete probability distribution. For example, when you want to use the normal to approximate a binomial.
Watch the video for an example:
According to the Central Limit Theorem, the sample mean of a distribution becomes approximately normal if the sample size is “large enough.” for example, the binomial distribution can be approximated with a normal distribution as long as n*p and n*q are both at least 5. Here,
- n = how many items are in your sample,
- p = probability of an event (e.g. 60%),
- q = probability the event doesn’t happen (100% – p).
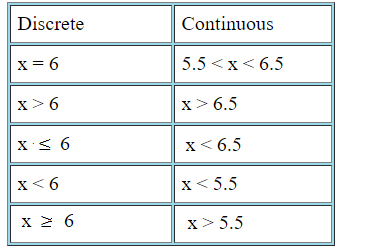
The continuity correction factor accounts for the fact that a normal distribution is continuous, and a binomial is not. When you use a normal distribution to approximate a binomial distribution, you’re going to have to use a continuity correction factor. It’s as simple as adding or subtracting .5 to the discrete x-value: use the following table to decide whether to add or subtract.
Continuity Correction Factor Table
Need help with the table? Check out our tutoring page!
- If P(X=n) use P(n – 0.5 < X < n + 0.5)
- If P(X > n) use P(X > n + 0.5)
- If P(X ≤ n) use P(X < n + 0.5)
- If P (X < n) use P(X < n – 0.5)
- If P(X ≥ n) use P(X > n – 0.5)
Let’s make the table a bit more concrete by using x = 6 as an example. The column on the left shows what you’re looking for (e.g. the probability that x = 6), while the right-hand column shows what happens to 6 after the continuity correction factor has been applied.
Continuity Correction Factor Example
The following example shows a worked problem where you’ll actually use the continuity correction factor to solve a probability problem using the z-table.
Example problem: If n = 20 and p = .25, what is the probability that X ≥ 8?
Step 1: Figure out if your sample size is “large enough”. Start by working out n*p and n*q:
np = 20 * .25 = 5 (note: this is also the mean x̄)
nq = 20 * .75 = 15
These are both over 5, so we can use the continuity correction factor.
Step 2: Find the variance of the binomial distribution:
n*p*q = 20 * .25 * .75 = 3.75
Set this number aside for a moment. You’ll use this value in Step 4 to find a z-score.
Step 3: Use the continuity correction factor on the X value. For this example, we have a greater than or equals sign (≥), so the table tells us:
P(X ≥ n) use P(X > n – 0.5)
X ≥ 8 becomes X ≥ 7.5.
Step 4: Find the z-score. You’ll need all three values from above:
- The mean (x̄) from Step 1,
- The variance (s) from Step 2,
- The Xi value from Step 3.
Step 5: Look up Step 4 in the z-table.
1.29 = .4015.
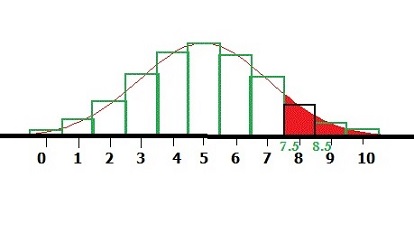
Step 6: Subtract Step from .5 to get the area (we are looking for the right tail in the above image):
.5 – .4015 = 0.0985.
The probability that X ≥ 8 is 0.0985.
Why is the continuity correction factor used?
While the normal distribution is continuous (it includes all real numbers), the binomial distribution can only take integers. The small correction is an allowance for the fact that you’re using a continuous distribution.
Check out our Youtube channel, where you’ll find tons of videos to help with stats.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.