What is a Random Sample?
A random sample is a sample that is chosen randomly. It could be more accurately called a randomly chosen sample. Random samples are used to avoid bias and other unwanted effects. Of course, it isn’t quite as simple as it seems: choosing a random sample isn’t as simple as just picking 100 people from 10,000 people. You have to be sure that your random sample is truly random!
Note that the word “random” in random sample doesn’t exactly fit the dictionary definition of the word. If you Google “define:random” then you’ll read that it means:
made, done, happening, or chosen without method or conscious decision.
“a random sample of 100 households”
It isn’t true that a random sample is chosen “without method of conscious decision.” Simple random sampling is one way to choose a random sample.
What is a Simple Random Sample?
A simple random sample is often mentioned in elementary statistics classes, but it’s actually one of the least used techniques. In theory, it’s easy to understand. However, in practice it’s tough to perform.
Technically, a simple random sample is a set of n objects in a population of N objects where all possible samples are equally likely to happen. Here’s a basic example of how to get a simple random sample: put 100 numbered bingo balls into a bowl (this is the population N). Select 10 balls from the bowl without looking (this is your sample n). Note that it’s important not to look as you could (unknowingly) bias the sample. While the “lottery bowl” method can work fine for smaller populations, in reality you’ll be dealing with much larger populations.
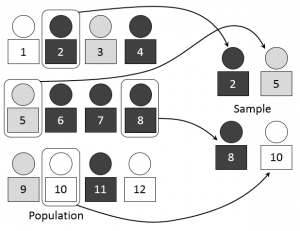
Imagine the people illustrated in the image above are game pieces. Place the 12 game pieces in a bowl and (again, without looking) choose 3. This is simple random sampling.

The simplest example of SRS would be working with things like dice or cards — rolling the die or dealing cards from a deck can give you a simple random sample. But in real life you’re usually dealing with people, not cards, and that can be a challenge.
How to Perform Simple Random Sampling: Example
A larger population might be “All people who have had strokes in the United States.” That list of participants would be extremely hard to obtain. Where would you get such a list in the first place? You could contact individual hospitals (of which there are thousands and thousands…) and ask for a list of patients (would they even supply you with that information? If you could somehow obtain this list then you will end up with a list of 800,000 people which you then have to put into a “bowl” of some sort and choose random people for your sample. This type of situation is the type of real-life situation you’ll come across and is what makes getting a simple random sample so hard to undertake.
Example question: Outline the steps for obtaining a simple random sample for outcomes of strokes in U.S. trauma hospitals.
Step 1: Make a list of all the trauma hospitals in the U.S. (there are several hundred: the CDC keeps a list).
Step 2: Assign a sequential number to each trauma center (1,2,3…n). This is your sampling frame (the list from which you draw your simple random sample).
Step 3: Figure out what your sample size is going to be. See: (Sample size) (how to find one).
Step 4: Use a random number generator to select the sample, using your sampling frame (population size) from Step 2 and your sample size from Step 3. For example, if your sample size is 50 and your population is 500, generate 50 random numbers between 1 and 500.
Warning: If you compromise (say, by not including ALL trauma centers in your sampling frame), it could open your results to bias.
Simple Random Sample vs. Random Sample
A simple random sample is similar to a random sample. The difference between the two is that with a simple random sample, each object in the population has an equal chance of being chosen. With random sampling, each object does not necessarily have an equal chance of being chosen. Unequal probability sampling isn’t usually addressed in basic statistics courses.
Square Root Biased Sampling
Square root biased sampling isn’t a technique that’s widely used, and it’s doubtful that you’ll be tested on it in any elementary statistics or AP statistics class. That said it is an interesting technique that attempts to address the problem of profiling at airport screenings.
I get selected for “extra screening” every time I travel by plane. I’m guessing it’s because I have dreadlocks, but I really have no idea. All I know is something about me is causing security to pull me aside every time. As well as it not being fair, it’s also taking up resources that could be better spent looking at other people who might actually be up to terrorist activities!
Statisticians strive to choose random people for surveys and experiments. This random sampling doesn’t happen at airport screenings, presumably because people who “look” a certain way are more likely to be terrorists. This is a problem William H. Press attempts to address with square root biased sampling. He states:
“…resources are wasted on the repeated screening of higher probability, but innocent, individuals.”
In other words, profiling by ethnicity, having the same name as someone on a watch list (or in my case, having dreadlocks) isn’t a mathematically sound way to catch a terrorist.
Square root biased sampling adds simple random sampling to profiling. Simple random sampling is where individuals are chosen completely by chance from a population. The addition of SRS increases the chance a guilty person will be found. It should also mean innocent travelers are more likely to breeze through security. The system works by assigning the same profiling. Instead of a profiled passenger being selected for screening every time, they may be pulled aside less frequently. For example, if a person is 10 times more likely to be a terrorist, the current system would pull them aside ten times more often than a non-profiled passenger. This basically means every time that profiled person travels they will be pulled aside. The addition of SRS means that the passenger will only be pulled aside three times as often.
Other ways to get a random sample:
Stratified random sample
Single-stage cluster sampling
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
William Press.