Statistics Blog > sigma / sqrt (n)
You’ll come across a couple of different formulas when calculating z-scores:
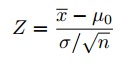
![]()
When I first started learning statistics, the different formulas completely confused me. They still do (a little) and I have to think about what I’m doing every time I calculate a z-score. In order to figure out which formula to use, and why we use sigma / sqrt (n), I tried to really understand what I was doing by asking questions:
Q. When do I use sigma /sqrt(n)?
A. You always divide by sqrt(n). However, occasionally the square root of n sometimes equals 1 (making it just σ in the denominator. for example, if you are choosing one person and trying to figure out the probability their weight is under x pounds, then n=1. In other words, if you are calculating a z-score, you can always use √(n).
Q. Why do we have to use sigma / sqrt(n)?
When you are estimating the standard error, SE, for the mean (the SE is the standard deviation of the means of samples), the larger your sample size, the smaller the standard deviation. for example, if you took a sample of 200, you would be much more likely to get close to the true mean than if you took a sample of 2. In other words, the larger your “n”, the smaller the standard deviation.
To see a visualization of this fact, try out this applet, which shows you how the sampling distribution of the sample mean approaches a normal distribution (you can also visualize how the sample standard deviation gets smaller as n gets larger.
Need a mathematical proof? Dr.Math gave an excellent answer to the question of proof. You can read the response here.