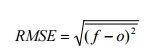What is Root Mean Square Error (RMSE)?
Root Mean Square Error (RMSE) is the standard deviation of the residuals (prediction errors). Residuals are a measure of how far from the regression line data points are; RMSE is a measure of how spread out these residuals are. In other words, it tells you how concentrated the data is around the line of best fit. Root mean square error is commonly used in climatology, forecasting, and regression analysis to verify experimental results.
- f = forecasts (expected values or unknown results),
- o = observed values (known results).
The bar above the squared differences is the mean (similar to x̄). The same formula can be written with the following, slightly different, notation (Barnston, 1992):
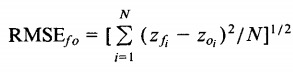
Where:
- Σ = summation (“add up”)
- (zfi – Zoi)2 = differences, squared
- N = sample size.
You can use whichever formula you feel most comfortable with, as they both do the same thing. If you don’t like formulas, you can find the RMSE by:
- Squaring the residuals.
- Finding the average of the residuals.
- Taking the square root of the result.
That said, this can be a lot of calculation, depending on how large your data set it. A shortcut to finding the root mean square error is:
![]()
Where SDy is the standard deviation of Y.
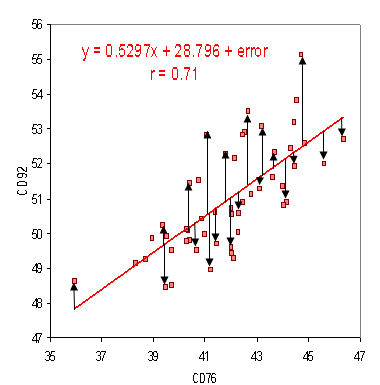
When standardized observations and forecasts are used as RMSE inputs, there is a direct relationship with the correlation coefficient. For example, if the correlation coefficient is 1, the RMSE will be 0, because all of the points lie on the regression line (and therefore there are no errors).
References
Barnston, A., (1992). “Correspondence among the Correlation [root mean square error] and Heidke Verification Measures; Refinement of the Heidke Score.” Notes and Correspondence, Climate Analysis Center. Available from here.
Kenney, J. F. and Keeping, E. S. “Root Mean Square.” §4.15 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 59-60, 1962.