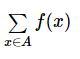Contents:
- What is a Probability Mass Function?
- Probability Mass Function Equations: Examples
- Tables and Graphs
- Formal Definition
What is a Probability Mass Function?
Watch the video for an overview and a few examples, or read on below:
A probability mass function (PMF)— also called a frequency function— gives you probabilities for discrete random variables. “Random variables” are variables from experiments like dice rolls, choosing a number out of a hat, or getting a high score on a test. The “discrete” part means that there’s a set number of outcomes. For example, you can only roll a 1, 2, 3, 4, 5, or 6 on a die.
Its counterpart is the probability density function, which gives probabilities for continuous random variables.
A PMF can be an equation, a table, or a graph.
Probability Mass Function Equations: Examples
A PMF equation looks like this:
P(X = x).
That just means “the probability that X takes on some value x”.
It’s not a very useful equation on its own; What’s more useful is an equation that tells you the probability of some individual event happening. For example:
P(X = 1) = 0.2 * 0.2.
How you come up with these equations depends mostly on what type of event you have. For example, the binomial distribution PMF is:
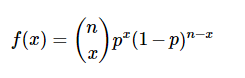
And the Poisson distribution PMF is:
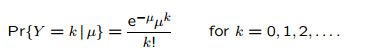
Need help with a homework question? Check out our tutoring page!
Tables and Graphs
The histogram is just a graph of a PMF.
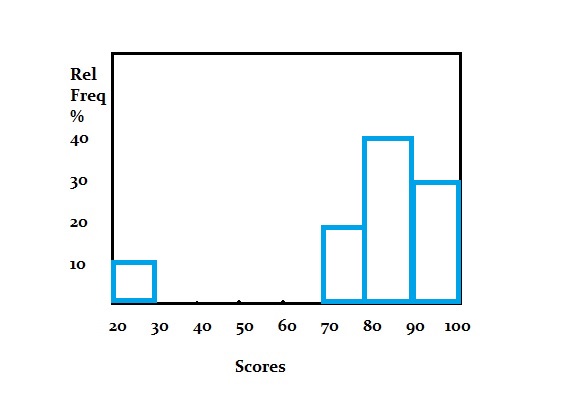
On the x-axis are the discrete random variables; On the y-axis are the probabilities for each discrete variable. The area under a curve of a probability mass function is 100% (i.e. the probability of all events, when added together, is 100%). The above histogram shows:
- 10% of people scored between 20 and 30,
- 20% of people scored between 70 and 80,
- 40% of people scored between 80 and 90, and
- 30% of people scored between 90 and 100.
That gives a total of 10% + 20% + 40% + 30% = 100%.
Another example:
The following table and graph show the PMF for an experiment. Note how all of the probabilities add up to 1:
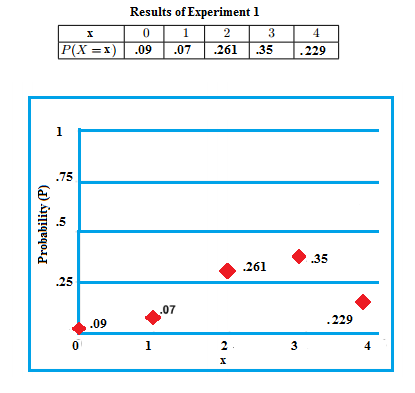
Formal Definition
Like many mathematical terms, there’s the informal definition (given above), and then there’s the formal one:
The probability mass function, f(x) = P(X = x), of a discrete random variable X has the following properties:
- All probabilities are positive: fx(x) ≥ 0.
- Any event in the distribution (e.g. “scoring between 20 and 30”) has a probability of happening of between 0 and 1 (e.g. 0% and 100%).
- The summation of all probabilities is 100% (i.e. 1 as a decimal): Σfx(x) = 1.
- An individual probability is found by adding up the x-values in event A. P(X Ε A) =
Where Σ is summation notation.
Terminology note
The general use of the term PMF means a probability distribution for a discrete random variable. However, some authors (not many) use the term “probability mass function” to mean either a discrete or continuous probability distribution. To add to the confusion, other authors might call a PMF a probability function or frequency function. Make sure you know the author’s intent when reading a textbook.
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.