Statistics Definitions > Geometric Mean
Contents.
Basics:
More Advanced Info:
- Equal Ratios and a Geometric Explanation.
- Logarithmic Values and Dealing with Negative Numbers.
- Arithmetic Mean-Geometric Mean Inequality
- Antilog of a Geometric Mean
Geometric Mean Definition and Formula
Watch the video for three examples of how to find the geometric mean:
The geometric mean is a type of average , usually used for growth rates, like population growth or interest rates. While the arithmetic mean adds items, the geometric mean multiplies items. Also, you can only get the geometric mean for positive numbers.
Like most things in math, there’s an easy explanation, and there’s a more, ahem, mathematical way of stating the same thing. Formally, the geometric mean is defined as “…the nth root of the product of n numbers.” In other words, for a set of numbers {xi}Ni=1, the geometric mean is:
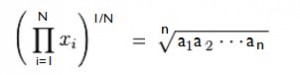
What this formula is saying in English is: multiply your items together and then take the nth root (where n is the number of items).
The π symbol in the formula is product notation: It’s the mathematical notation for “product”, similar to the (probably more familiar) Σ in summation notation.
How to Find the Geometric Mean (Examples)
Need help with a homework question? Check out our tutoring page!
Example 1: What is the geometric mean of 2, 3, and 6?
First, multiply the numbers together and then take the cubed root (because there are three numbers) = (2*3*6)1/3 = 3.30
Note: The power of (1/3) is the same as the cubed root 3√. To convert a nth root to this notation, just change the denominator in the fraction to whatever “n” you have. So:
- 5th root = to the (1/5) power
- 12th root = to the (1/12) power
- 99th root = to the (1/99) power.
Example 2: What is the geometric mean of 4,8.3,9 and 17?
First, multiply the numbers together and then take the 5th root (because there are 5 numbers) = (4 * 8 * 3 * 9 * 17)(1/5) = 6.81
Example 3: What is the geometric mean of 1/2, 1/4, 1/5, 9/72 and 7/4?
First, multiply the numbers together and then take the 5th root: (1/2*1/4*1/5*9/72*7/4)(1/5) = 0.35.
Example 4: The average person’s monthly salary in a certain town jumped from $2,500 to $5,000 over the course of ten years. Using the geometric mean, what is the average yearly increase?
Solution:
Step 1: Find the geometric mean.
(2500*5000)^(1/2) = 3535.53390593.
Step 2: Divide by 10 (to get the average increase over ten years).
3535.53390593 / 10 = 353.53.
The average increase (according to the GM) is 353.53.
Tip: The geometric mean of a set of data is always less than the arithmetic mean with one exception: if all members of the data set are the same (i.e. 2, 2, 2, 2, 2, 2, then the two means are equal.
A More Detailed Example

Let’s say you own a piece of art that increases in value by 50% the first year after you buy it, 20% the second year, and 90% the third year. What these numbers tell you is that at the end of the first year the value was multiplied by 150% or 1.5, the second year the value at the end of year 1 was multiplied by 120% or 1.2 and at the end of the third year the value at the end of year 2 was multiplied by 190% or 1.9. As these are multiplied, what you are looking for is the geometric mean which can be calculated in the following way:
(1.5*1.2*1.9)(1/3) = 1.50663725458… or about 1.51
What the answer of 1.51 is telling you is that if you multiplied your initial investment by 1.51 each year, you would get the same amount as if you had multiplied it by 1.5, 1.2 and 1.9.
- Art work value year 0: $90,000.
- Art work value year 1: $90,000 * 1.5 = $135,000
- Art work value year 2: $135,000 * 1.2 = $162,000
- Art work value year 3: $90,000 * 1.9 = $307,000
or, using the geometric mean:
$90,000 * 1.506637254583 = $307,000*
*If you do this calculation, it’s slightly different because of the number of decimal places I wrote here. In other words, you should get the exact result on a calculator.
Why not use the Arithmetic Mean Instead?
The arithmetic mean is the sum of the data items divided by the number of items in the set:
(1.5+1.2+1.9)/3 = 1.53
As you can probably tell, adding 1.53 to your initial price won’t get you anywhere, and multiplying it will give you the wrong result.
$90,000 * 1.53 * 1.53 * 1.53 = $322,343.91
Technology Options for Calculating the GM
- JMP does not have a formula, but you can create one with the formula editor.
- SAS: If you use SAS/STAT 12.1 or later, specify the ALLGEO statistic keyword in the PROC SURVEYMEANS statement. Earlier editions lack this capability.
- Excel: use the GEOMEAN function for any range of positive data. The syntax is GEOMEAN(number1, [number2], …)
- SPSS: Use the MEANS command. In the SPSS menus, choose Analyze>Compare Means>Means, then click on the “Options” button and select from the list of available statistics on the left.
- MINITAB: use the GMEAN function. The syntax is GMEAN(number), where “number” is the column number. All numbers must be positive.
- MAPLE: The calling sequence GeometricMean has a variety of options for calculating the mean from a data sample (A), a matrix data set(M) or a random variable or distribution(X). See this article for the full parameters.
- TI83: there is no built in function. As a workaround, enter your data into a list and then enter the geometric mean formula on the home screen.
- TI89: like the TI83, there isn’t a built in function. You could install an app, like the “Statistics and Probability Made Easy” app, which I recommend as I used it in grad school :).
Real Life Uses
Aspect Ratios
The geometric mean has been used in film and video to choose aspect ratios (the proportion of the width to the height of a screen or image). It’s used to find a compromise between two aspect ratios, distorting or cropping both ratios equally.
Computer Science
Computers use mind-boggling amounts of data which often has to be summarized using statistics. One study compared the precision of several statistics (arithmetic means, geometric means, and percentage in the top x%) for a mind-boggling 97 trillion pieces of citation data. The study found that the geometric mean was the most precise (see this Cornell University Library article).
Geometry
1. Mean Proportional
The geometric mean is used as a proportion in geometry (and is sometimes called the “mean proportional”). The mean proportional of two positive numbers a and b, is the positive number x, so that:
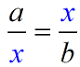
In this image, triangles ADC, ADB, and CAB are similar.
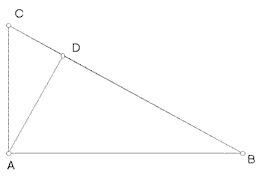
If you have similar triangles, you can use the proportion to find missing sides. For example, the leg rule states that: hypotenuse/leg = leg/projection. These types of problems appear in high school geometry classes.
2. Golden Ratio
The golden mean has a value of about 1.618 and can be derived from the geometric mean and similar rectangles. Let’s say you have a rectangle with width “a” and length “b”. Create a square within the rectangle with sides “a”:
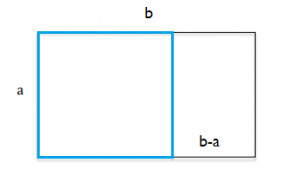
The smaller rectangle to the left is similar to the larger rectangle. Both rectangles contain the golden ratio, which is the ratio of the rectangle’s length to width. You could write a statement about the relationship between the two rectangles:
b : a = a : b – a
This statement, a proportional statement about the rectangles, also defines the geometric mean as “a”.
Medicine
The Geometric Mean has many applications in medicine. It has been called the “gold standard” for some measurements, including for the calculation of gastric emptying timesJNM.
Proportional Growth
As the examples at the beginning of this article demonstrate, the geometric mean is useful for calculating proportional growth, like the growth seen in long term investments using the Treasury bill rate as your riskfree rate (the riskfree rate is the theoretical return rate on a risk free investment). According to NYU corporate finance and valuation professor Aswath Damodoran, the geometric mean is appropriate for estimating expected returns over long term horizons. For short terms, the arithmetic mean is more appropriate.
It’s use isn’t limited to financial markets—it can be applied anywhere there is some type of proportional growth. For example, let’s say the amount of cells in a culture are 100, 180, 210, and 300 over a four day period. This gives a growth of 1.8 for day 2, 1.167 for day 3, and 1.42 for day 4. The geometric mean is (1.8 * 1.167 * 1.42)(1/3) = 1.44, meaning a daily growth of .44 or 44%.
United Nations Human Development Index
The Human Development Index (HDI) is an index that takes into account factors other than economic development when reporting a country’s growth. It is “…a summary measure of average achievement in key dimensions of human development: a long and healthy life, being knowledgeable and have a decent standard of living. The HDI is the geometric mean of normalized indices for each of the three [categories].”UNDP
The “normalized” indexes refer to the fact that the geometric mean isn’t affected by differences in scoring indices. For example, if standard of living is scored on a scale of 1 to 5 and longevity on a scale of 1 to 100, a country that scores better in longevity would score better overall if the arithmetic mean were used. The geometric mean isn’t affected by those factors.
Water Quality Standards
Test results for water quality (specifically, fecal coliform bacteria concentrations) are sometimes reported as geometric means. Water authorities identify a threshold geometric mean where beaches or shellfish beds must be closed. According to CA.GOV, the dampening effect of the geometric mean is especially useful in water quality calculations, as bacteria levels can vary from 10 to 10,000 fold over a period of time.
Back to Top
Equal Ratios
When you look at the geometric mean and the numbers you put into the calculation, an interesting thing happens. Let’s say you wanted to find the geometric mean of 4 and 9. The calculation would be √(4 * 9) = 6.
- The ratio of the first number (4) and the geometric mean (6) is 4/6, which reduces to 2/3.
- The ratio of the second number (9) and the geometric mean (6) is 6/9, which reduces to 2/3.
As you can see, the ratios are the same. This tells you that the geometric mean is a sort of “average” of all of the multipliers you are putting into the equation. Take the numbers 2 and 18. What number could you put in the center so that the ratio of 2 (to this number) is the same as the ratio of this number to 18?
2 (?) 18
If you guessed 6, you’re right, because 2 * 3 = 6 and 6 * 3 = 18. For more complex numbers, the ratios would be difficult to work out, which is why the formula is used.
You can get the same result (6) by using the formula, so if you’re ever presented the above type of problem in a math class, just find the square root of the numbers multiplied together:
√(2 * 18) = 6
A Geometric Explanation
Let’s say you had a rectangle with sides of 2″ and 18″. The perimeter of this rectangle has the same perimeter as a square with four sides of 10″ each. 10 is what you would get if you worked out the arithmetic mean:
(2 + 18) / 2 = 20 / 2 = 10.
The geometric mean can also be equated to the rectangle-square scenario: the square root of the sides (i.e. √ 2*18) is the length of the sides of a square with the same area as the rectangle. A rectangle 2″ x 18″ = 36 square inches and 6″ x 6″ is also 36 square inches. 6 is what you would get if you worked out the geometric mean: √(2*18) = 6.
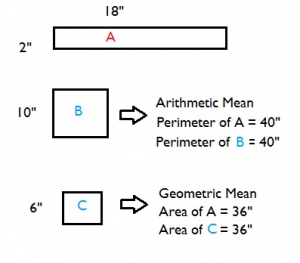
Similarly, the geometric mean of three numbers a, b, and c is a cuboid with sides a, b, and c equal to the three numbers.
Logarithmic Values and the Geometric Mean
One way to think of the geometric mean is that it’s the average of logarithmic values converted back to base 10. If you’re familiar with logarithms, this can be a very intuitive way to look at it. For example, let’s say you wanted to calculate the geometric mean of 2 and 32.
Step 1: Convert the numbers to base 2 logs (you can theoretically use any base):
- 2 = 21
- 32 = 25
Step 2:Find the (arithmetic) average of the exponents in Step 1. The average of 1 and 5 is 3. We’re still working in base 2 here, so our average gives us 23, which gives us the geometric mean of 2 * 2 * 2 = 8.
Dealing with Negative Numbers
Generally, you can only find the geometric mean of positive numbers. If you have negative numbers (common with investments), it’s possible to find a geometric mean, but you have to do a little math beforehand (which is not always easy!).
Example: What is the geometric mean for an investment that shows a growth in year 1 of 10 percent and a decrease the next year of 15 percent?
Step 1: Figure out the total amount of growth for the investment for each year. At the end of the first year you have 110% (or 1.1) of what you started with. The following year, you have 90% (or 0.9) of what you started year 2 with.
Step 2: Calculate the geometric mean based on the figures in Step 1:
GM = √(1.1 * 0.9) = 0.99.
The geometric mean for this scenario is 0.99. Your investment is slowly losing money at a rate of about 1% per year.
Arithmetic Mean-Geometric Mean Inequality
The Arithmetic Mean-Geometric Mean Inequality (AM-GM inequality) states that for a list of non-negative real numbers, the arithmetic mean is greater than or equal to the geometric mean. Taking the formulas for both types of mean, we get the inequality:
![]()
For example, for the sequence of numbers {9, 12, 54}, the arithmetic mean, 25, is greater than the geometric mean, 18. The multiple proofs of this inequality are beyond the scope of this statistics site, but Bjorn Poonen offers this simple one line proof for the AM-GM inequality with two variables:
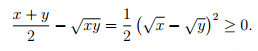
Antilog of a Geometric Mean
The antilog of a number is raising 10 to its power. Let’s say your geometric mean is 8. Raise base 10 to 8:
108
The general formula is:
antilog(g) = 10g = 10√(a*b)
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Poonen, B. Retrieved March 3, 2023 from: http://mathcircle.berkeley.edu/BMC4/Handouts/inequal.pdf
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.