What is a Cumulative Distribution Function (CDF)?
The cumulative distribution function (also called the distribution function) gives you the cumulative (additive) probability associated with a function.
For example, the CDF for a continuous random variable is the integral:
![]()
It is an extension of a similar concept: a cumulative frequency table, which measures discrete counts. With a table, the frequency is the amount of times a particular number or item happens. The cumulative frequency is the total counts up to a certain number:
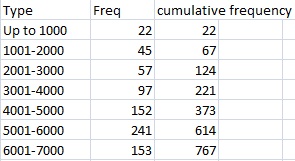
The cumulative distribution function works in the same way, except with probabilities.
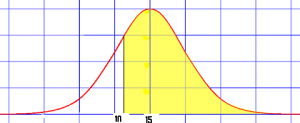
You can use the CDF to figure out probabilities above a certain value, below a certain value, or between two values. For example, if you had a CDF that showed weights of cats, you can use it to figure out:
- The probability of a cat weighing more than 11 pounds.
- The probability of a cat weighing less than 11 pounds.
- The probability of a cat weighing between 11 and 15 pounds.
In the case of the above scenario, it would be important for, say, a veterinary pharmaceutical company knowing the probability of cats weighing a certain amount in order to produce the right volume of medications that cater to certain weights.
Cumulative Distribution Functions in Statistics
The cumulative distribution function gives the cumulative value from negative infinity up to a random variable X and is defined by the following notation:
F(x) = P(X ≤ x).
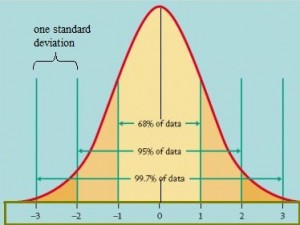
This concept is used extensively in elementary statistics, especially with z-scores. The z-table works from the idea that a score found on the table shows the probability of a random variable falling to the left of the score (some tables also show the area to some z-score to the right of the mean). The normal distribution, the basis of z-scores, is a cumulative distribution function:
References
Abramowitz, M. and Stegun, I. A. (Eds.). “Probability Functions.” Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 925-964, 1972.
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, pp. 6-8, 2000.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 92-94, 1984.
UVA: Image Retrieved April 29, 2021 from: http://www.stat.wvu.edu/srs/modules/normal/normal.html