A credible interval is the interval in which an (unobserved) parameter has a given probability.
It’s the Bayesian equivalent of the confidence interval you’ve probably encountered before. However, unlike a confidence interval, it is dependent on the prior distribution (specific to the situation). In confidence intervals we also treat the parameter as a fixed value, and the bounds are random variables; in credible intervals, the estimated parameter is treated as a random variable while the bounds are considered fixed.
Examples of Credible Intervals
Suppose we are running an experiment on the distribution of birth weights of children born in a given town. If the subjective probability that the birthweight β is somewhere between 2.8 kgs and 3.5 is 90 %, we can say that 2.8 ≤ β ≤ 3.5 is a 90% credible interval.
If you find out that the 95% credible interval for your statistics final score is 70 to 90, this means you have a 95% chance of having a score between those two numbers.
Technical Definition of a Credible Interval
Remember that an alpha level, α, defines the amount of uncertainty; the probability that we support the alternate hypothesis when really, the null hypothesis is true. We can say that our 100 (1 – α) % credible interval C defines the subset on the parameter space, which we’ll call θ, such that the integral
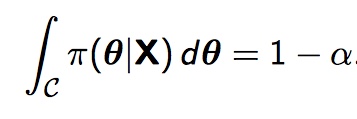
π here is the posterior probability distribution. So, for instance, if you needed a 95 percent credible interval, you would be working to find the interval over which the integral of the posterior probability distribution sums to 0.95.
There’s one shortcut we can sometimes take. If the parameter space θ is a discrete space — that is, if we’re working with a set of discrete data points rather than a continuous distribution– we can sum over our interval rather than take an integral.
References
Hitchcock, David. Bayesian Inference: Posterior Intervals (Stat 535 Lecture Notes)
Retrieved from http://people.stat.sc.edu/Hitchcock/stat535slidesday3.pdf on February 16, 2018
Jaynes, E. T. (1976). “Confidence Intervals vs Bayesian Intervals”, in Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, pp. 175 et seq. Retrieved from http://bayes.wustl.edu/etj/articles/confidence.pdf on February 17, 2018