A Bayesian estimator is an estimator of an unknown parameter θ that minimizes the expected loss for all observations x of X.
In other words, it’s a term that estimates your unknown parameter in a way that you lose the least amount of accuracy (as compared with having used the true value of that parameter).
Bayes Estimators & The Loss Function
A bayesian estimator is a function of observable random variables, variables you observed in the process of your research. Call your observable variables X1 X2…Xn
Your data may be able to be represented by the function f(x|θ), where θ is a prior distribution. However, you don’t know the actual value of θ, so you have to estimate it. An estimator of θ is a real valued function δ(X1… Xn), not to be confused with Δx in calculus, which means a small change.
The loss function L(θ, a) where a ε R, is also a real valued function of θ. Our estimate here is a, and L(θ, a) tells us how much we lose by using a as an estimate when the true, real value of a parameter is θ.
There are different possible loss functions. For instance, the squared error loss function is given by L(θ a) = (θ –a)2. The absolute error loss function would be L(θ a) = |θ –a|.
In the first definition of Bayesian estimator at the beginning of this page, we said it was an estimator that minimized expected loss. That loss is represented by a loss function like one of those we’ve just described.
We can find the minimum expected loss by integrating. For a given X = x, the expected loss (E) is:
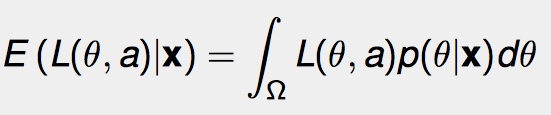
In this formula the Ω is the range over which θ is defined. p(θ | x) is the likelihood function; the prior distribution for the parameter θ over observations x. Call a * (x) the point where we reach the minimum expected loss. Then, for a*(x) = δ*(x), δ*(x) is the Bayesian estimate of θ.
Bayesian Estimator: References
Brynjarsdottir, Jenny. STAT 611 Lecture Notes: Lecture 12, Estimation.
Retrieved from https://www2.stat.duke.edu/courses/Fall12/sta611/Lecture12.pdf on March 9, 2018
Shiryaev, A. N. Bayesian estimator, Encyclopedia of Mathematics. Retrieved from : http://www.encyclopediaofmath.org/index.php?title=Bayesian_estimator&oldid=19043 on March 4, 2018.
Zhu, Wei. Bayesian Inference for the Normal Decision. Retrieved from http://www.ams.sunysb.edu/~zhu/ams571/Bayesian_Normal_wide.pdf on March 4, 2018