A tangent space is a generalization to manifolds of the simple idea of a tangent as applied to two-dimensional curves.
A manifold is a topological space that, near every point, can be modeled on Euclidean space.
- One dimensional manifold includes lines and curves.
- Two-dimensional manifolds are surfaces: spheres and cylinders are both examples.
One way to imagine it is to think of tangent space of a point x on a manifold to be a vector space that contains every possible direction you could tangentially pass through x; a surface that contains every tangent vector of that point.
A tangent space has the same number of dimensions as its manifold does. If we put together all the tangent spaces of every point on the manifold, we get the tangent bundle. A tangent bundle has twice the dimension of the original manifold.
Example of a Tangent Space.
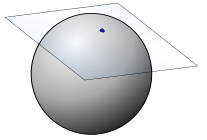
The image above shows one manifold you are very familiar with: the sphere. It can be described by the equation
![]()
Where our point of interest is p = (0,0,0). Then the line
![]()
will be tangent to our sphere at the point p, and every vector (a,b,0) will be a tangent vector of our sphere at the point p. Remember that the collection of all tangent vectors to a manifold at a given point is the tangent space.
References
Wijsman, Robert A. Invariant Measures on Groups and Their Use in Statistics. Chapter 3. Differentiable Manifolds, Tangent Spaces, and Vector Fields. Institute of Mathematical Statistics, 1990. Lecture Notes – Monograph Series. Retrieved from https://projecteuclid.org/download/pdf_1/euclid.lnms/1215540658 on June 25, 2019.