Shannon entropy (or just entropy) is a measure of uncertainty (or variability) associated with random variables. It was originally developed to weigh the evenness and richness of animal and plant species (Shannon, 1948). It’s use has expanded to many other areas including:
- Information theory, which considers stochastic processes as sources of information,
- Nutrition, where the Shannon Entropy Diversity Metric measures diversity in a diet,
- Physics, where thermodynamic entropy is a special case of Shannon entropy (Lent, 2019) and can also be used to measure information in some types of wave functions (Wan, 2015).
How to Calculate Shannon Entropy
Exactly how you calculate entropy is very field specific. For example, you wouldn’t calculate nutrition in the same way you calculate entropy in thermodynamics. However, all formulas are based on Shannon’s original metric, which was calculated as follows:
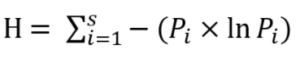
Where:
- H = Shannon Entropy,
- Pi = fraction of population composed of a single species i,
- ln = natural log,
- S = how many species encountered,
- Σ = summation of species 1 to S
References
INDDEX Project (2018), Data4Diets: Building Blocks for Diet-related Food Security Analysis. Tufts University, Boston, MA. https://inddex.nutrition.tufts.edu/data4diets. Accessed on 26 August 2020.Lent, C. (2019). Information and Entropy in Physical Systems. Retrieved August 26, 2020 from: https://www.springerprofessional.de/en/information-and-entropy-in-physical-systems/16000644
Patrascu, V. (2017). Shannon entropy for imprecise and under-defined or over-defined information. Retrieved August 26, 2017 from: http://arxiv-export-lb.library.cornell.edu/abs/1709.04729v1
Shannon, C. (1948). A Mathematical Theory of Communication. Bell System Technical Journal Volume 27, Issue 3.
Wan, J. (2015). S.E. as a Measurement of the Information in a Multiconfiguration Dirac—Fock Wavefunction. Chinese Physics Letters 32(2):023102
DOI: 10.1088/0256-307X/32/2/023102