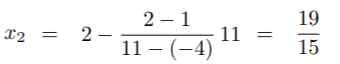Secant Method: Definition, Example

Calculus Definitions >

The secant method is a derivative-free method for finding roots of a univariate function. It’s useful when you don’t want to (or can’t) use derivatives.

General Steps

The general idea is that you pick two points close to the actual solution (these are generally denoted x₁ and x₂ or, equivalently, x_i and x_{i – 1}. Then, draw a secant line between those two points. The approximation for the root will be where the secant line crosses the x-axis:


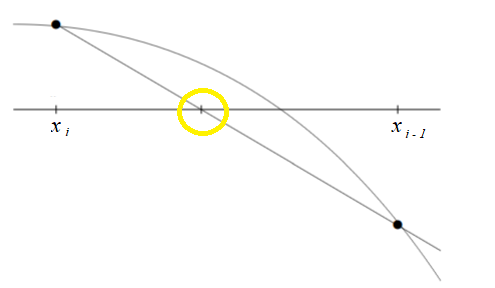
The point where the secant line crosses the x-axis is used as a new second point in an iterative process for finding the root.

Formulas for the Secant Method

If you don’t know the derivative of a function, you can use the secant method to try and find a root by interpolation. The difference quotient approximates the derivative with:

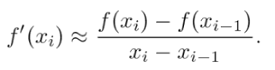
The root is where f(x) = 0, so you:

1. Plug your values for x_i and x_i-1 into the formula,
2. Set y = 0,
3. Solve for x,
4. Use that value for x in the next iteration.

The iteration formula is (Gomes, 2009):

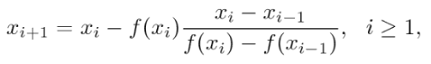
For example, let’s say you wanted to find the root for f(x) = x⁴ – 5.

1. Make a guess for your initial points: (1, 2).
2. Find the function values at those points:
   • f(1) = 1⁴ – 5 = -4
   • f(2) = 2⁴ – 5 = 11
3. Plug your values into the formula:
   
   
4. Plug your value from Step 3 into the function to find its value at that point (x₃:
   • f(19/15) = (19/15)⁴ – 5 ≈ 1.267
5. Use (x₂, x₃) in the next iteration, repeating the steps above (from 2 onward).

Using Technology

You probably won’t have to work the formulas by hand, because many applications have built in functions (you will have to make an initial guess, which you can usually obtain by graphing the function). For example, in R (Asar, 2020):

secant(fun, x0, x1, eps, maxit = 20, silent = FALSE)
Where:

• fun = the function you’re trying to find the root for,
• x0 = first value (initial guess)
• x1 = second value (initial guess)
• eps = tolerance for the algorithm’s convergence
• maxit = maximum number of iterations
• silent = logical statement which decides if the iterations should be printed (or not)

If you do have to work the process by hand, the following video walks you through an example:

Secant Method Advantages and Disadvantages

It tends to give better results than the regula-falsi (false position) method (Jain, 2003). It also usually converges faster than the bisection method.

One disadvantage of the secant method is that, unlike the regula-falsi method, it doesn’t always converge (Jain, 2003). In addition, the method will fail if, at any stage, f(x_n) = f(x_{n – 1}).

References

Asar, O. (2020). Secant: A Function To Find Roots Of Univariate Functions. Retrieved August 8, 2020 from: https://www.rdocumentation.org/packages/OOmisc/versions/1.2/topics/secant
Gomes, A. (2009). Implicit Curves and Surfaces: Mathematics, Data Structures and Algorithms. Springer London.
Jain, M. Numerical Methods For Scientific And Engineering Computation. New Age International (P) Limited.
Young, T. (2020). Lecture 6: Secant Methods. Retrieved August 8, 2020 from: http://www.ohiouniversityfaculty.com/youngt/IntNumMeth/lecture6.pdf