The sample proportion (p̂) describes the proportion of individuals in a sample with a certain characteristic or trait. To find the sample proportion, divide the number of people (or items) who have the characteristic of interest by the total number of people (or items) in the sample. For example, let’s say you were conducting a survey of 100 people asking about whether they shop local or not. If 35 people say they shop local, then
p̂ can take on values between 0 and 1 (i.e., 0% to 100%).
Sample Proportion as a Random Variable
The sample proportion is a random variable because it varies randomly from sample to sample; if you were to survey a different set of 100 people, you might get anywhere from 0 positive responses (people who live in food deserts are unlikely to shop local) to 100 (people in planned towns might have no reason to travel for shopping). When we view the sample proportion as a random variable, it is denoted with a capital P: P̂.
As this statistic is a random variable, it may equal the population proportion, or it may not. However, your samples will cluster around the true population proportion; If the true proportion of people who shop locally was 0.40, the sample proportion will approach this number as you take more and more samples. If you had the time and money to sample everyone, then p = p̂ = 0.40;. It makes sense then, that the mean of the sample proportion is equal to the population proportion.
Standard Deviation of the Sample Proportion
If you randomly sample many times with a large enough sample size—so that you see at least five of each possible outcome—, the standard deviation equals [1]:
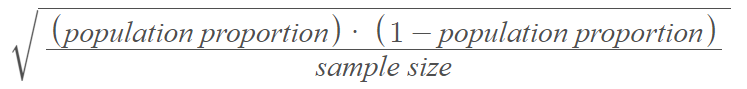
If you take many samples under the above conditions, the graph of the sample proportion will take on a bell shape. More formally, we say that the sampling distribution of the sample proportion is approximately normally distributed.
Next: Sampling Distribution of the Sample Proportion
References
[1] Rule of sample proportions. Retrieved February 4, 2021 from: http://personal.psu.edu/drh20/016/fall2010/psu016confint.pdf