What is a Quadruple Integral?
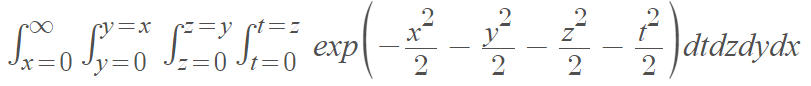
A quadruple integral is commonly described as an integral for finding hypervolumes of four-dimensional shapes.

Let’s say a box in 4-D space has coordinates (x, y, z, w). You could break the box up into equally-sized sub-boxes in the same way that you could divide the area under a curve into rectangles. However, with a 2D curve, we’re only making rectangles in one direction (on the x-axis). With four-dimensional space we would have to make sub-boxes in four directions: x, y, z, and w. The quadruple integral over the box is the limit as these sub-boxes go to infinity [1].
Practical Applications of the Quadruple Integral
Despite seeming a little obscure, these integrals actually have a wide range of practical and useful applications in math and physics, including [2]:
- Asymptotic expansions, which describes a function’s asymptotic behavior in terms of a sequence of gauge functions
- Classical derivations of the Compton effect (an unusual result observed when X-rays are elastically scattered on some materials by electrons),
- Calculating the average distance between two points in a circle,
- Four-dimensional Fourier transform of a function of spacetime.
- Integrating over a Lagrangian density (used in quantum field theory),
- Some radiation impedance calculations (radiation impedance is, roughly speaking, potential quantity to a flow quantity),
- Finding hypervolumes—the content of objects in four-dimensional space.
In fact, the quadruple integral can be used anywhere you have a physical system with four variables. The system doesn’t necessarily have to be four-dimensional — it could be a system with two spatial coordinates and two particles.
References
Hypersphere image: Like bowser,
[1] Reynolds, R. & Stauffer, A. A Quadruple Definite Integral Expressed in Terms of the Lerch Function. Symmetry 2021, 13, 1638. https://doi.org/10.3390/ sym13091638
[2] Rowan, J. (2018). Math 53 Summer 2018 Homework Assignment 20 Solutions to selected problems.
[3] Symbolab Multiple Integrals Calculator.