How do I Convert a Z Score to Percentile?
A z-score gives you an idea of how far from the mean a data point is. Z-scores range from -3 standard deviations up to +3 standard deviations As a percentage, a z score of zero is 50%. But how do you calculate these conversions? Watch the video to view three ways to convert Z-scores to percentiles or vice versa (percentiles to z-scores):
Three Ways to Convert a Z-Score to Percentile (and Vice Versa)
To convert from one unit to another, use a calculator, like the one below, or use a table (see instructions further down) and calculate the percentile by hand. In either case, you will be more easily able to convert between units if you know some basics about normal distributions, like the 68 95 99.7 rule. This rule states that 68 percent of the area under a bell curve lies between -1 and 1 standard deviations either side of the mean, 94 percent lies within -2 and 2 standard deviations and 99.7 percent lies within -3 and 3 standard deviations; these standard deviations are the “z scores.”
The calculator below allows you to convert z-scores to percentiles:
To convert a percentile to a z-score, use this calculator.
Need help? Check out our tutoring page!
Convert Scores with a Z Table
A Z Table has z scores and their associated areas. Once you have found the area, convert that to a percentile. This mini table shows the area for z scores in .5 increments:
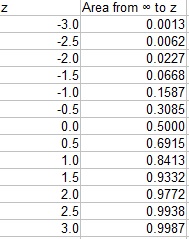
For example, let’s say you wanted to convert a z score of -2 to a percentile. The area listed in the table is .0227. To convert this decimal to a percentile, move the decimal point two places to the right and then add a percentage sign:
.0227 becomes 2.27%
Things become a little more tricky when you want a z score that’s not listed in the table above. In that case, you should use a more comprehensive z-table.
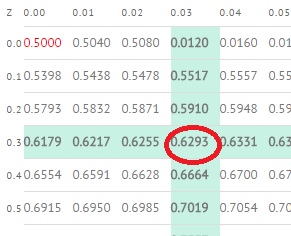
Z Score to Percentile Example
- Look up the value in the left hand z-table (see image above). The area is .6293.
- Move the decimal point two places to the right, then add a percentage sign: 62.93%.
Check out our YouTube Channel for hundreds of elementary statistics videos!
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.