Pre-Test and Post-Test Probability

RCT >

Pre-test and post-test probability refers to the probability of having a disease before a diagnostic test is performed (pre-test probability) and after a test is performed (post test probability).

How to Determine Pre-Test and Post-Test Probability

There are many different ways to calculate pre-test and post-test probability.

The pre-test probability is simply the prevalence of disease in a population. Pre-test probability is sometimes calculated by clinical judgment or data at hand (for example, practice data). One relatively simple way to find it in a particular population is to calculate the probability of patients who have the disease. This can be accomplished with the formula (Tape, n.d.):

P(D+) = (True Positives + False Negatives) / (True Positives + False Positives + True Negatives + False Negative)

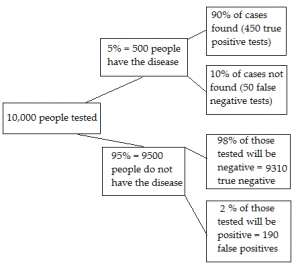
Applying Bayes theorem is an option for calculating probabilities; the post-test probability depends not only on the test’s accuracy but also on the pre-test probability of disease (Stoller & Michota, 2009), which in Bayes theorem terminology is called prior probability. Predictive values can be used to determine pre-test and post-test probability. Predictive values can be calculated if you know the test’s sensitivity and specificity and the estimated pretest disease probability.

Example of Post-Test Probability Using Likelihood Ratios

An alternative method is to use a likelihood ratio (LR), which combines sensitivity and specificity into a single number (Fiebach & Barker, 2007). This method is fairly straightforward (at least, compared to Bayes theorem), but you do have to work through several steps. Parikh et al. (2009) give a thorough example of how to do this. The steps are summarized below:

1. Collect your pre-test probability. For this example, let’s assume that’s 2.5%.
2. Find the sensitivity and specificity of the test. Let’s say published data gives you sensitivity of 60%, specificity of 97%.
3. Calculate the LR. LR = Sensitivity / 1- specificity = 0.6 / 0.03 = 20
4. Calculate the pretest odds using the formula: Pretest odds = pretest probability / (1-pretest probability). Giving 0.025 / 0.975 = 0.03.
5. Find the posttest odds. Posttest odds = pretest odds * LR = 0.03 * 20 = 0.6
6. Finally, calculate the post-test probability by dividing the posttest odds by the posttest odds + 1: .6/ 1.6 = 0.375 or 37.5%.

References

Fiebach, M. & Barker, L. (2007). Principles of Ambulatory Medicine. Lippincott Williams & Wilkins.
Parikh, R. et al. (2009). Likelihood ratios: Clinical application in day-to-day practice. Indian J Ophthalmol.
Stoller, J. & Michota, F. (2009). The Cleveland Clinic Intensive Review of Internal Medicine Fifth Edition. Lippincott Williams & Wilkins.
Tape, T. Basic Concepts and Definitions. Retrieved May 4, 2019 from: http://gim.unmc.edu/dxtests/reviewof.htm