Factoring limits Examples

Limit of functions >

Factoring limits is a way to find limits by canceling common factors. Usually, you’ll want to try direct substitution first. If you end up with an indeterminate limit like 0/0, try using factoring to turn the function into one where you can use substitution.

Factoring Limits Examples

Example #1: Find the limit of the following function by factoring:

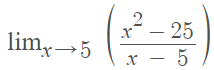
Step 1: Factor the numerator, denominator, or both (this depends on what is factorable in your expression). For this example, we’re factoring the numerator, x² – 25:

1. Rewrite 25 as 5²: x² – 5²: (x² – 5²)
2. Apply the difference of two squares formula from algebra (x² – y² = (x + y)(x – y): (x + 5)(x – 5).

Step 2: Replace the factored parts of the expression back in the formula:

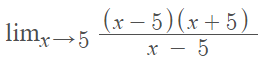
Step 3: Cancel like terms. For this example, we have (x – 5) in the numerator and denominator so we can cancel both of those out:


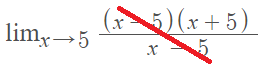
Which leaves:

Step 4: Use substitution to solve. For this example, plug 5 (the term specified by the “lim” expression) into the formula on the right (x + 5):

(5 + 5) = 10.

The limit is 10.

Example #2: Find the limit of the following function by factoring:

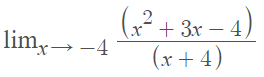
Step 1: Factor the numerator, denominator, or both (this depends on what is factorable in your expression). For this example, we can factor the numerator:

1. Break into groups: (x² + 3x – 4) = (x² – x) + (4x – 4)
2. Factor out x from x² – x: x(x – 1)
3. Factor out 4 from 4x – 4: 4(x – 1)
4. Combine the above two expressions: x(x – 1) + 4(x – 1)
5. Factor out the common term (x – 1): (x – 1)(x + 4)

Step 2: Replace the factored parts of the expression back in the formula:

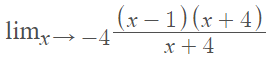
Step 3: Cancel like terms.

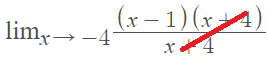
Step 4: Use substitution to solve.
lim_x→-4 (x – 1) = -5.

References

7. Limits by algebraic simplification. Retrieved July 14, 2021 from: https://web.auburn.edu/holmerr/1617/Textbook/limbyalg-screen.pdf