Randomized Clinical Trial > Bipartite matching
Matching places participants in observational studies into comparable, homogeneous groups or strata at the beginning of a study. It is one way to avoid selection bias (Cochran and Chambers, 1965). Matching designs can be bipartite matching, or non-bipartite matching, which are terms borrowed from graph theory.
Bipartite Matching
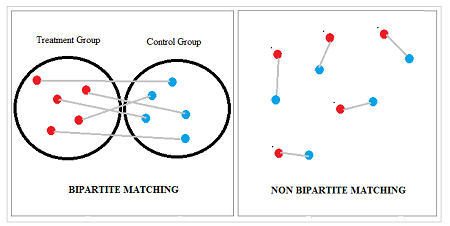
Bipartite matching—also called conventional two-group matching—creates pairs from two distinct groups. On the left in the above image, connections are made between the treatment and controls. Bipartite matching is equivalent to sampling without replacement.
Graphically, in bipartite matching you would match each node in the treatment group to a single node from the control group. A node is a point or circle (red in the left image, blue on the right). It is the fundamental unit from which graphs are made. The match is represented by an edge in the graph. An edge is a line that connects two nodes. A weight is assigned to each edge; Basically, this weight is the difference for some aspect of the pairs, like difference in age, height, or BMI. Well matched pairs in bipartite matching ideally have very little difference between them. Therefore, smaller weights are preferable. Although the concept is simple (i.e. create matched pairs with the smallest differences), the calculations are not—especially if you have multiple covariates. Algorithms like the Greedy Matching Algorithm have been developed to create ideal weights between nodes.
One drawback to this type of matching is that it can only be used for fairly simple designs.
Non-Bipartite Matching
A non-bipartite design—or multi-group matched design—produces pairs from multiple groups. It is equivalent to sampling with replacement. Bipartite designs are more common, but non-bipartite designs are available for the rare case when you want to reuse a member; For example, if you use the same control as a match for two or more treatment group participants.
In the above graph, each node in the right hand box is in a separate group. Non-bipartite matching is available for when you want to reuse a member; For example, if you use the same control as a match for two or more treatment group. Augmenting path algorithms like the Blossom V algorithm (available here) are available for creating non-bipartite matches. They are technically complex, which may be a reason why biparite matches are often preferred.
Bipartite Matching Problems
A matching in an undirected graph is a collection of edges with no common endpoints. A perfect bipartite matching is matches all vertices and although bipartite matching sounds easy, it is not. Multiple scenarios are possible, some of which may be “easier” than others.
References
Cochran WG, Chambers SP. The Planning of Observational Studies of Human Populations. Journal of Royal Statistical Society, Ser A. 1965;128:234–266.
Lu et. al. Optimal Non bipartite matching and Its Statistical Applications. Am Stat. 2011; 65(1): 21–30.
Shakti, P. (2023). Hard distribution.
Wolfram. Bipartite Graph.