Calculus Definitions > Cavalieri’s Principle
What is Cavalieri’s Principle?
Cavalieri’s principle is a way to compare solids in 3-dimensional space. For example, the following three objects all have the same volume:
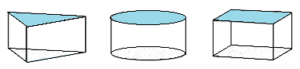
Cavalieri’s principle simplifies calculating an area for a prism or cylinder: find a box that is similar to the prism or cylinder, and calculate the volume for that instead. It’s much easier to solve the box formula (l * w * h) than:
- πr2h (the cylinder formula) or
- 1/2 * a * c * h (the prism formula)
Note that the prism formula basically involves finding a box anyway, then dividing by one half.
The principle is named after Bonaventura Cavalieri, one of Galileo’s students. It holds for:
- Cuboids: including disjoint unions of a finite set of cuboids, as long as they have sides that are parallel to their axes.
- Cylinders,
- Prisms (solids with flat sides and identical ends), whether right-angled or oblique.
Example
Let’s say you want to prove that the following pyramid and cone have the same volume.
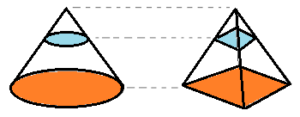
Steps
The basic steps are:
- Place the two solids on an imaginary plane (you could imagine that you’re simply placing them on a table). In the above image, the solids are placed on an orange-colored imaginary plane.
- Draw an imaginary slice (i.e. another plane) through the solid, so that each plane is parallel to the original plane. In the above picture, I’ve drawn a blue plane.
- Continue to draw slices through the objects. Make sure to include the very top of your solids, the very bottom, and a few slices in between. You can draw as any as you want, but the more, the better.*
- Check that Every one of the planes in one solid also intersects the other. Basically, this is telling you, in a roundabout way, that the height of the two solids is the same.
* Technically, you should draw an infinite number of planes, just in case there’s a plane that doesn’t have the same area (in which case, the solids won’t have the same volume). If you’re doing this by hand, it’s only practical to draw a few. Also, sometimes you only have to check three planes. For example, a cube’s planes are identical in length and width, by definition.
Proof
Many proofs exist for Cavalieri’s principle. The following proof (from Rotman’s Journey into Mathematics: An Introduction to Proofs) uses double integrals. You start by finding a circular area (R) using a grid of squares. When you know R, it’s a small leap to find the area of an ellipse (R’).
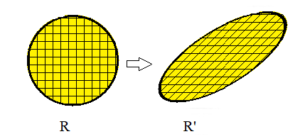
As long as the horizontal cross sections (i.e. rows of squares) have the same length, the squares can be oriented to form the parallelograms in the ellipse. From basic geometry, the theorem for the area of a parallelogram states:
Theorem: the area of a parallelogram with base b and height h is A = bh
You can use this theorem to make the conclusion that the area of R equals the area of R’.
The main point of the exercise is that calculating with circles is a lot easier than dealing with ellipses—even if you’re throwing double integrals into the mix, it’s very easy to visualize the proof.
References
Rotman, J. (2013). Journey into Mathematics: An Introduction to Proofs. Courier Corporation.
Wheeden and A. Zygmund, Measure and Integral — An Introduction to Real Analysis. Chapman and Hall/CRC; 2 edition (April 24, 2015)