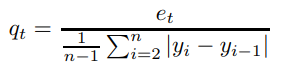What is Mean Absolute Scaled Error?
Mean Absolute Scaled Error (MASE) is a scale-free error metric that gives each error as a ratio compared to a baseline’s average error.
The advantages of MASE include that it never gives undefined or infinite values and so is a good choice for intermittent-demand series (which arise when there are periods of zero demand in a forecast). It can be used on a single series, or as a tool to compare multiple series.
MASE is defined by the following equation:
MASE = mean ( | qt | ) ~ Prestwich et. al, 2013
Where:
- t = 1…n is the set of forecasting sample periods.
Comparison of Mean Absolute Scaled Error to Other Metrics
Mean Absolute Scaled Error (MASE) is one of four main measures of forecasting accuracy. The other three are:
- Scale-dependent methods: e.g. Mean absolute error (MAE or MAD). Although these are easy to calculate, they can’t be used to compare different series, because of the scale dependency.
- Percentage-error methods: e.g. Mean Absolute Percent Error (MAPE); These can be used to compare different series because they are scale independent. However, they can’t be used when you have zeros in your data.
- Relative-error methods: averages error ratios from a chosen metric to that of a naive one. These metrics can’t be used when you have small errors, because the resulting calculations would involve division by zero.
Rob Hydman, in his Foresight article Another look at forecast-accuracy metrics for intermittent demand states that the mean absolute scaled error is the only method out of the four that “…always gives sensible results.” However, Prestwich et. al do note that you can’t use it when every in-sample demand is identical.
References
Hyndman, R. (2006) Another look at forecast-accuracy metrics for intermittent demand.
Prestwich, S. et al. (2013). Mean-Based Error Measures for Intermittent Demand Forecasting. Retrieved July 29, 2019 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.741.9979&rep=rep1&type=pdf