A leminiscate is a shape traditionally drawn with polar coordinates.
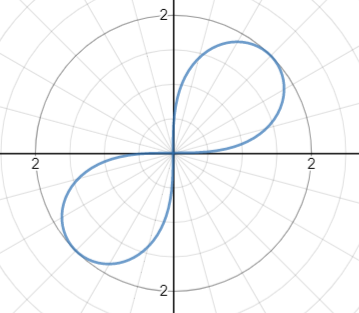
The equation for the leminiscate is r2 = a cos 2θ or r2 = a sin 2θ. Changing a will shrink or expand the shape (to try out different values, check out the interactive leminiscate page at Desmos.com).
Alternatively, the shape can be given as a set of points in a Cartesian plane so that (Piene, 2007)
- x = (sin t) / (1 + cos2t) and
- y = (sin t cos t) / (1 + cos2t).
Area of a Leminiscate
You can find the area inside a loop with integrals.
Example question: Find the area inside one loop of a leminiscate r2 = 4 cos 2θ.
Solution:
Step 1: Find the limits of integration. Perhaps the easiest way to do this is to graph one loop. Note that instead of graphing y2 = 4 cos 2θ (which is pretty impossible with most graphing calculators), you can graph y = ±2√(cos 2x) instead:
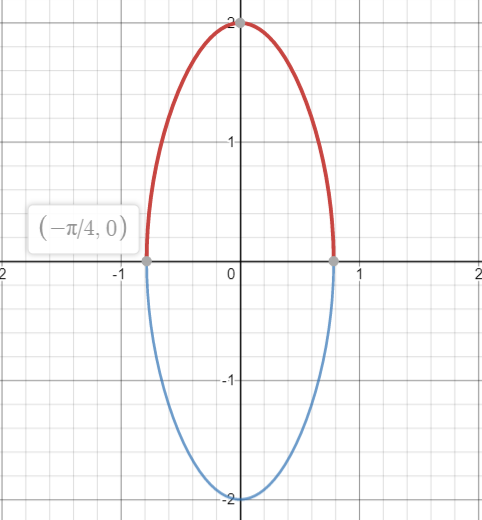
Using the trace function, we can see that one loop is traced out for θ in the interval
−π/4 < θ < π/4 (or 3π/4 < x < 5π/4).
Step 2: Integrate the function r2 = 4 cos 2θ, using the limits of integration found in Step 1. We’re only finding the area for a single loop here, so the integral needs to be halved:
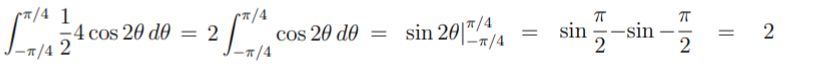
The area for one loop is 2.
References
Graph of the leminiscate: Desmos.com.
Piene, R. (2007). Curves and Surfaces. Retrieved May 20, 2020 from: https://www.ima.umn.edu/materials/2006-2007/T4.13-14.07/837/Piene_IMA_07_v2.pdf
White, D. (2014). Quiz 9A, Math 1860-021 Solutions. Retrieved December 3, 2020 from: http://www.math.utoledo.edu/~dwhite1/d_1860/q9a1860s1.pdf