Linearly Independent Solutions in Systems of Equations
Linearly independent solutions can’t be expressed as a linear combination of other solutions.
If f(x) and g(x) are nonzero solutions to an equation, they are linearly independent solutions if you can’t describe them in terms of each other. In math terms, we’d say that and is no c and k for which the expression
c f(x) + k g(x) = 0
is true.
Using a Graph to Find Linearly Independent Solutions
One way of figuring out if a set of solutions to a system of equations is linearly independent is to graph them. Independence in a system of linear equations means that the two equations will only meet at a single point. In other words, if the two equations are linearly independent, they will cross at exactly one place. Linear dependent solutions will either be parallel to each other or turn out to be actually the same line.
Suppose 4x + 2y = 6 and y = -x – 2 were your two solutions. Graphed, they become:
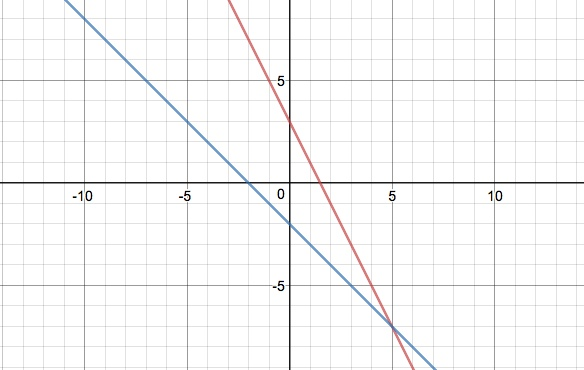
Since they cross in just one place, they are linearly independent solutions.
The Wronskian Function and Differential Equations
For differential equations, you can use linear independence to find all of the solutions for a particular problem. For example, the following equation is a second order differential equation:
y′′ + 9y = 0
As a differential equation of order 2, its solution has two linearly independent solutions.
One way of defining linear independence in this context is simply that two functions are “different”. This isn’t as easy as it sounds: two functions that look different might actually be the same. For example although cos(x) and cos(-x) look different, they are actually the same function [1]. One tool to show that one function is linearly independent from another is the Wronskian.
There is a special function called the Wronskian which can tell you whether two solutions (or functions of any sort) are linearly independent or not. The Wronskian W is defined as:
W (f, g)(t) = f(t) g′(t) – g(t) f′(t).
Where:
- f and g are functions of t,
- gf′(t) is the first derivative of g,
- ff′(t) is the first derivative of f.
Suppose two functions f and g are differentiable on some interval I.
- If W(f, g) (x) = 0 for all x in the interval I, the two functions are linearly dependent on I.
- If W(f, g) (x) &≠ 0 for some x0 in the interval I, then the two functions are linearly independent.
As a simple example of this, let’s take a look two functions:
- f(t) = 2 t2 and
- g(t) = t4.
The Wronskian would be
f(t) gf′(t) – g(t) ff′(t) = 2 t2 · 4 t3 – t5 · 4t = 4t5.
Since this is not zero for some t (in fact, for all t except 0, the two functions are linearly independent.
References
[1] Math 21 – Spring 2014. Classnotes, Week 8. Retrieved July 13, 2021 from: https://web.stanford.edu/class/archive/math/math21/math21.1146/files/21/notes8.pdf
Thomas, Weir, & Hass. Thomas’ Calculus, Chapter 17. Retrieved from http://www.math.wisc.edu/~passman/Thomas12e_WebChap17.pdf on November 17, 2018.
Math 54: Linear independence and the Wronskian. Retrieved July 13, 2021 from: https://math.berkeley.edu/~lindsey/math54_linear_independence_wronskian
Chapter 2: The General, Linear Equation. Retrieved July 13, 2021 from: http://people.cs.uchicago.edu/~lebovitz/Eodesbook/lin.pdf