Falling Power: Definition

Calculus Definitions >

What is a Falling Power?

A falling power (also called a falling factorial) is formally defined as:


The expression n^k is “n to the k falling” (note the important underline in the exponent). The notation n^k is commonly used in combinatorics; Some authors do use other notation. For example, Loeb (1992) uses (x)_n [1].

The first few falling powers are [2]:

• n⁰ = 1
• n¹ = n
• n² = n(n – 1) = n² – n
• n³ = n(n – 1)(n – 2) = n³ – 3n² + 2n
• n⁴ = n(n – 1)(n – 2)(n – 3) = n⁴ – 6n³ + 11n² – 6n

Conversion from Ordinary Powers

Falling powers are analogous to regular powers in finite calculus and differential calculus [3].In general, ordinary powers like x² or x³ can be expressed as linear combinations of falling powers; You can convert from ordinary powers to falling powers by using Stirling numbers:



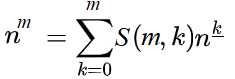
Where “S” is a Stirling number of the second kind.

Examples:

• n² = S(2, 2)n² + S(2, 1)n¹ + S(2, 0)n⁰ = n (n – 1) + n
• n³ = S(3, 3)n³ + S(3, 2)n² + S(3, 1)n¹ + S(3, 0)n⁰ = n (n – 1)(n – 2) + 3n(n – 1) + n
• n⁴ = S(4, 4)n⁴ + S(4, 3)n³ + S(4, 2)n² + S(4, 1)n¹ + S(4, 0)n⁰
  = n(n – 1)(n – 2)(n – 3) + 6n(n – 1)(n – 2) + 7n(n – 1) + n

Usefulness of Falling Powers

Falling powers are commonly used in the calculus of finite differences and arise in several different areas including generating functions, hypergeometric functions and power series solutions to differential equations.

References

[1] Loeb, D. (1992). A generalization of the Stirling numbers. In Discrete Mathematics 103, 259-269. North-Holland.
[2] Catone, C. Bringing Calculus into Discrete Math via the Discrete Derivative. The College Mathematics Journal, 50:1, 21-27, DOI: 10.1080/07468342.2019.1530553. Retrieved June 11, 2021 from: http://www.auemath.aichi-edu.ac.jp/teacher/kodani/lecture/zemi-r2/matsubara.pdf
[3] Rosen, K. (2017). Handbook of Discrete and Combinatorial Mathematics. CRC Press.