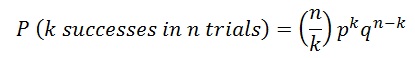Probability and Statistics > Ti 83 for Statistics > Difference Between BinomPDF and BinomCDF
Contents:
Difference Between BinomPDF and BinomCDF: Overview
Watch the video for an overview:
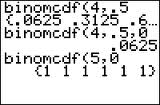
BinomPDF and BinomCDF are both functions to evaluate binomial distributions on a TI graphing calculator. Both will give you probabilities for binomial distributions. The main difference is that BinomCDF gives you cumulative probabilities.
BinomPDF
BinomPDF is the probability that there will be X successes in n trials if there is a probability p of success for each trial. For example, if if n = 10, p = .5, and x = 3 the BinomPDF will return .117. That means there is a .117 (11.7%) chance that there will be 3 successes.
Use BinomPDF when you have questions that have:
- An exact number, like: all, half, none, or a specific number X.
BinomCDF
This function is exactly the same as BinomPDF except that instead of a specific number of successes (i.e. “3 trials”) this function gives you the probability there will be 0 to x successes in n trials. In other words, if you put X=3 it will five you the probability for 0,1,2 and 3 trials (all together). For example, if you input the same numbers as the BinomPDF example above (n = 10, p = .5, x = 3) you’ll get .172 (17.2%) with BinomCDF. This percentage is higher as it’s adding up all of the probabilities to X=3, much in the same way that you add probabilities in a cumulative frequency distribution table.
Use BinomCDF when you have questions with wording similar to:
- No more than, at most, does not exceed.
- Less than or fewer than.
- At least, more than, or more, no fewer than X, not less than X.
- Between two numbers (run BinomCDF twice).
BinomCDF TI 83 Calculator: Overview
The TI 83 BinomPDF and TI 83 BinomCDF functions can help you solve binomial probability questions in seconds. Binomial probabilities involve two outcomes: Success or failure. For example, if you were tossing a coin to see how many heads you were going to get, if the coin landed on heads that would be a “success.” The difference between the two functions is that one (BinomPDF) is for a single number (for example, three tosses of a coin), while the other (BinomCDF) is a cumulative probability (for example, 0 to 3 tosses of a coin).
For single number probabilities (like two, or three, or a dozen, or something similar, you’ll want to use BinomPDF.
BinomCDF TI 83 Calculator: Steps
Watch the video for the steps:
Example problem: Bob’s batting average is .321. If he steps up to the plate four times, find the probability that he gets up to three hits.
Step 1: Press 2nd VARS to get the “DISTR” option. Scroll down to “A:BinomCDF” and then press ENTER.
Step 2: Enter the number of trials. Bob bats four times, so the number of trials is 4. Press 4 followed by a comma.
Step 3: Enter the Probability of Success, P. Bob has a batting average of .321, so enter .321 followed by a comma.
Step 4: Enter the X value. We want to know what the probability is that Bob will get up to three hits, so enter 3, followed by a close parenthesis.
Step 5: Press ENTER for the result. Bob’s chances of getting up to three hits is .989.
Tip: Instead of scrolling down to “A:BinomCDF” you can press ALPHA then MATH.
That’s how to use BinomCDF TI 83 Calculator!
Binomial Probability TI 83: BinomPDF.
This section tells you how to use the BinomPDF function to figure out an exact quantity (like three times, or twice, or a dozen occurrences). For cumulative probabilities (like “up to a certain number” or “between 5 and 10” or “under 6” or something similar, you’ll want to use BinomCDF.
Sample problem: Sue has a batting average of .270. If she is at bat three times, what is the probability that she gets exactly two hits?
Step 1: Press 2nd VARS to get the “DISTR” option. Press 0 for “binomPDF.”
Step 2: Enter the number of trials from the question. Sue bats three times, so the number of trials is 3. Press 3 and hit the , key.
Step 3: Enter the Probability of Success, P. Sue’s batting average is .270, so enter .270, then hit the , key.
Step 4: Enter the X value. We want to know Sue’s chances of getting exactly two hits, so enter 2 and then press ).
Step 5: Press Enter for the result. Sue’s chances of getting exactly two hits is .159651.
Warning: BinomialPdf is an exact probability for one value of x. If you want to find a cumulative probability (for example, what are John’s chances of getting 0 or 1 hits?) you will need the use the BinomCDF function.
That’s how to find a Binomial Probability on the TI 83!
Lost your guidebook? Download a new one here at the TI website.
Check out our Youtube channel for more stats help and tips!
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.