TI 83 > Critical z value TI 83
Critical z value TI 83
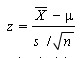
A critical value in a hypothesis test separates the rejection region (where the hypothesis will be rejected) from the region where the hypothesis will not be rejected. You could use the equation above to find the z-score; with a little arithmetic, you can look up a critical value in a z-table, or you can use the InvNorm function on the TI-83 graphing calculator.
Watch the video for an example:

Find more help for the TI 83 and statistics by visiting the main TI 83 for statistics menu.
Critical z value TI 83: Steps
InvNorm can be used in a couple of different ways. The first problem shows you how to find a critical value (a z-score) for a given alpha level for example, α = 0.05. The second problem shows you how to use InvNorm find a specific score for data with a normal distribution.
Example Problem #1: Find the critical z value for α = 0.05.
Step 1: Press 2nd VARS 3. This displays InvNorm( on the home screen.
Step 2: Type one of the following:
0.05 (for a one tailed test)
0.05/2 (for a two tailed test).
Not sure? See: One Tailed Test or Two.
Step 3: Press the ) button.
Step 4: Press Enter.
- -1.64 is the z-score for the left tail.
- 1.64 is the z-score for the right tail (because the normal distribution is a symmetrical distribution).
- -1.96 is the area in the left tail for a two tailed test
- 1.96 is the area in the right tail for a two tailed test (because the normal distribution is symmetrical).
Sample Problem #2: An end of semester exam is normally distributed with a mean of 85 and a standard deviation of 10. Find the score at the 90th percentile with the InvNorm function.
Step 1: Press 2nd VARS 3. This displays InvNorm( on the home screen.
Step 2: Type .90,85,10.
Step 3: Press the ) button.
Your display should read InvNorm(.9, 85, 1, 0).
Step 4: Press ENTER. This returns 97.82. That means that 90% of students will have scores below 97.82.
That’s it! Like the explanation?
That’s how to find a Critical z value TI 83!
Tip: The first entry on InvNorm should be a number between 0 and 1.
Lost your guidebook? Download a new one here from the TI website.
Check out our Youtube channel for more stats help and tips!
Comments are closed.