Minimum Spanning Tree > Boruvka’s Algorithm
What is Boruvka’s Algorithm?
Boruvka’s Algorithm is a way to find a minimum spanning tree — a spanning tree where the sum of edge weights is minimized. It was the first algorithm developed (in 1926) to find MSTs; Otakar Boruvka used it to find the most efficient routing for an electrical grid.
There are many ways to find minimum spanning trees. Boruvka’s Algorithm is a greedy algorithm and is similar to Kruskal’s algorithm and Prim’s algorithm. It is basically a cross between the two algorithms. It is also known as Sollin’s algorithm, especially in computing.
Boruvka’s Algorithm Example
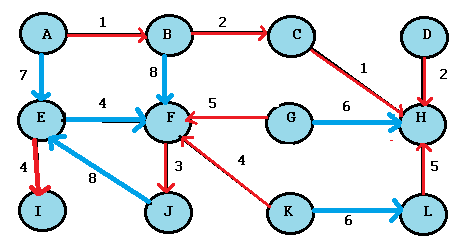
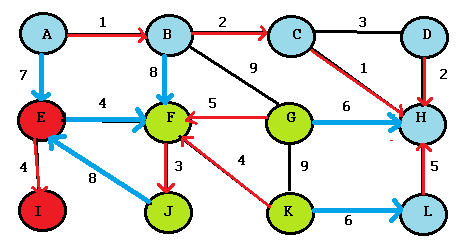
Find the minimum spanning tree for the following graph using Buruvka’s Algorithm.
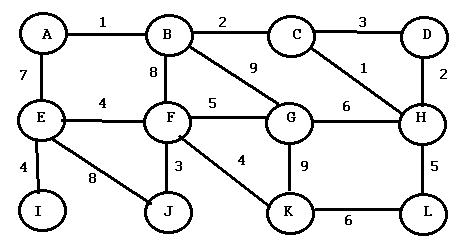
Step 1: Write out a list of components. For this graph, we have: A,B,C,D,E,F,G,H,I,J,K,L. This step is optional but helps you to keep track.
Step 2: Highlight the cheapest outgoing edge for each node in your list. For example, node A has outgoing edges with weights 1 and 7, so we’ll highlight 1. Continue sequentially (for this list, go to B, then C…).
Guidelines:
- At this stage, only highlight one cheapest edge for each node.
- For a tie (node E has two edges with a weight of 4), assign a lower weight to one of the edges. This is arbitrary, but must stay consistent throughout the process. For this example, I’ll make the edge to the left the lowest weight.
- Always highlight the cheapest edge, even if it has been highlighted before. Do not choose the edge with the next lowest weight! For practical purposes, this means you might not have to highlight anything for some nodes, if the cheapest weight has already been highlighted.
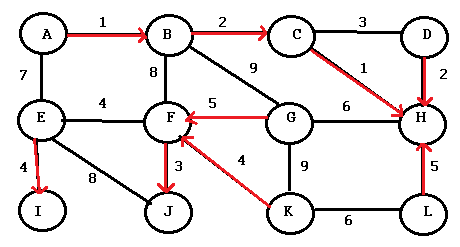
Step 3: Highlight the separate tree clusters. These are the sets of connected nodes, which we’ll call components.
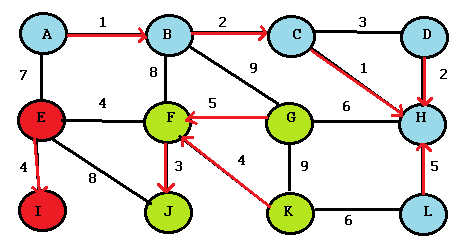
Step 4: Repeat the algorithm for each component (each differently colored set). This time, for each node, choose the cheapest edge outside of the component. For example, ABCDHL is one component (blue nodes). For node A, the cheapest edge outside the component is node 7 (because node 1 is connected inside the component). I’m highlighting in blue for clarity: you can use whatever color you like.
Guidelines:
- Make sure you are choosing the cheapest edge outside of the component. For this graph and this iteration, those edges are colored black.
- As in the first iteration, skip highlighting an edge if it’s already been highlighted this time around.
Step 5: If your nodes are all connected in a single component, you’re done. If not, repeat step 4.
The following graph shows the final MST. I’ve erased any unused (black) edges.