Probability > Total Probability Rule
What is the Total Probability Rule?
The total probability rule (also called the Law of Total Probability) breaks up probability calculations into distinct parts. It’s used to find the probability of an event, A, when you don’t know enough about A’s probabilities to calculate it directly. Instead, you take a related event, B, and use that to calculate the probability for A.
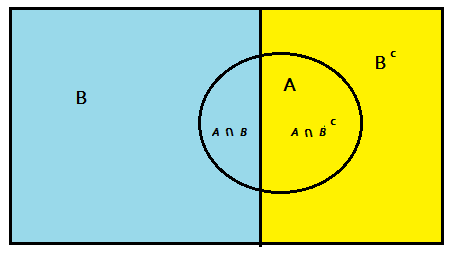
The probability for a can be written as sums of event B. The total probability rule is:
P(A) = P(A∩B) + P(A∩Bc).
Note: ∩ means “intersection” and Bc is the complement of B.
Need help with a homework question? Check out our tutoring page!
Using a Probability Tree to Find Total Probability
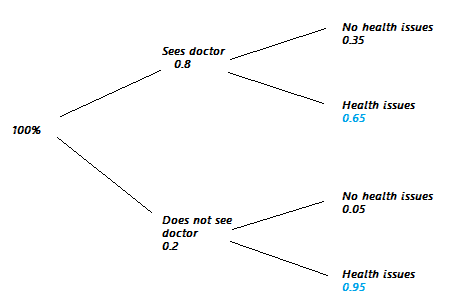
Example question: 80% of people attend their primary care physician regularly; 35% of those people have no health problems crop up during the following year. Out of the 20% of people who don’t see their doctor regularly, only 5% have no health issues during the following year. What is the probability a random person will have no health problems in the following year?
Step 1: Sketch out a tree. The following tree uses the information given in the question with the addition of two probabilities (in blue) obtained by the complement. For example, if 5% of people do not have health problems, that means 95% of people do have health problems.
Step 2: Multiply the probabilities for each branch. For example, the top branch has 0.8 on the first segment and 0.35 on the second. These calculations are shown in red on the graph below:
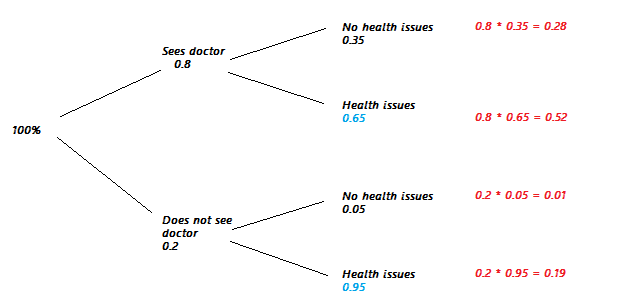
Step 3: Find the probabilities that answer the question. For this example, we want the probability a random person will have no health problems. If you look at the graph, the branches leading to “no health problems” are the top branch and the third branch down. The probabilities listed in red are 0.28 and 0.01, so the solution is:
0.28 + 0.01 = 0.29.
That’s it!
Using a Table to Solve for Total Probability
The idea is the same as the tree, only you put the data into a table format. This is less intuitive than the tree, even though it holds the same information. This first table holds the information given in the question:

Note that I only included in the table the information about “no health issues”, as that was what was being asked about in the question. You could include all of the information (including the people who had health issues), but that leads to complications in the next step (hence, it being less intuitive than the tree).
Next, the rows are multiplied to give joint probabilities:

The total probability rule is the basis for Bayes Theorem.
References
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.