The local derivative (also called the local time derivative or temporal derivative) tells us how a quantity changes in time at a fixed point in space [1]. It is a partial derivative with respect to time.
The notation for the local derivative is
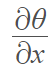
If the local derivative is equal to zero, that tells us the field is in a steady state [2].
Using vector notation,
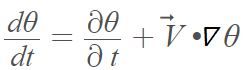
Describing change in θ at a fixed point (for example, a change in temperature at a fixed point in time):
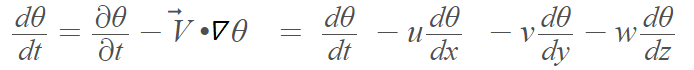
Where:
- ∇ is the del operator.
- (v·∇) is the convective derivative.
- The heavy middle dot is the dot product.
- d/dt is the total derivative, which is a summation of all partial derivatives.
The first application of the local derivative was made by Newton for general physics; the idea has been extended to many fields as diverse as image processing, structural optimization, and weather forecasting. However, it does have some limitations especially when applied to complex physical systems. These are best tackled with more advanced methods like fractional calculus or the beta derivative [3] (for example, see Riaz et. al).
Local Derivative vs. Convective Derivative
The convective derivative, also called a Lagrangian derivative and commonly used in classical and fluid mechanics, is a derivative taken with respect to a coordinate system (e.g., Cartesian, polar, …) moving with velocity u [4]. In steady flows, the local derivative is zero and only the convective derivative makes a contribution [5].
References
[1] Kiskis, J. Flow, etc. Retrieved March 4, 2022 from: http://kiskis.physics.ucdavis.edu/landau/phy9hb_old/flow.pdf
[2] Total Derivative. Retrieved March 4, 2022 from: http://people.atmos.ucla.edu/fovell/AOSC110_Spring2013/divergence_vorticity_notes.pdf
[3] Atangana, A. (2015). Derivative with a New Parameter. Theory, Methods and Applications. Elsevier Science.
[4] Convective Derivative. Retrieved March 4, 2022 from: https://www.chemeurope.com/en/encyclopedia/Convective_derivative.html#:~:text=The%20convective%20derivative%20(also%20commonly,fluid%20mechanics%20and%20classical%20mechanics.
[5] Fluids – Lecture 10 Notes. Retrieved March 4, 2022 from: https://web.mit.edu/16.unified/www/FALL/fluids/Lectures/f10.pdf