Contents:
- Scalar Definition
- Difference Between Scalar & Vector
- Scalar Function
- Scalar Field
- Scalar and Scalar Multiples in Linear Algebra
- Can a Scalar be Negative?
1. Scalar Definition
A scalar is a single real number that is used to measure magnitude (size). For example 10, -999 and ½ are scalars. An example of a scalar is length (which can be measured in inches or feet). A scalar represents magnitude, or the size of a mathematical object.
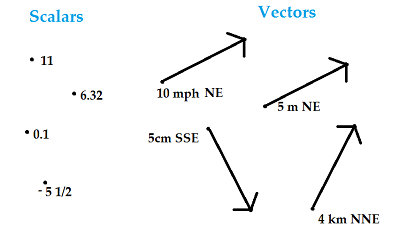
2. Difference Between Scalar & Vector
- Scalars have magnitude (i.e. a numerical value), but no direction.
- Vectors have both a magnitude and a direction.
Real numbers like -0.1, .001, 1, 1.435, √13 are always scalars in matrix and linear algebra**; they can’t be vectors without a direction.
Examples of scalars: 10 m; 100 degrees F; 222 K/cal
Examples of vectors: 5 m/sec North; 10 miles West;
**An exception: In physics, some real numbers can be vectors. See Can a Scalar be Negative? below.
3. Scalar Function
A scalar function is a function (of one or more variables) with one-dimensional scalar output. It may take in one or more variables, but it gives you a single value.
Another way of saying this is that the codomain of the function is exactly the set of real numbers. An n-variable scalar function is a map from the space Rn (an n-dimensional space) to the real number line. In math terminology, we’d write that as f: Rn -> R.
If a function isn’t scalar it is vector valued. A vector-valued function takes
scalars or vectors as inputs but outputs multi-dimensional vectors.
Scalar Function Examples
A function like f (x,y,z) = x2 + 4y + 2yz5 is a scalar function. This input of this function is three dimensional, but the output is just one dimensional: a scalar.
One dimensional functions like f(x) = 5x + 2 are scalar functions.
Use of Scalar Functions
You’ve come across these (relatively simple) kinds of functions throughout your algebra and calculus studies; they are important in all fields that use applied math. One example of these functions in use is in fluid mechanics. Often, the density and pressure of a fluid will vary with location, and we can describe the pressure and density distributions by using the Cartesian coordinates (x,y,z) and a scalar function. For example, the pressure variation would be written as p(x,y,z). It has a three-part, three-dimensional input, but the output is a scalar that describes the scalar at one exact point.
Directional Derivative of a Scalar Function
The directional derivative of a scalar function is defined as follows. Along a vector v, it is given by:
![]()
Where the rate of change of the function f is in the direction of the vector v with respect to time, at the point x.
4. Scalar Field
A scalar field is a function which assigns to every point of space a scalar value— either a real number or a physical quantity. Scalar fields are important in physics and are sometimes used with vector fields.
A scalar field is similar to a magnetic (or electromagnetic) field, except a scalar field has no direction.
Example of a Scalar Field
Perhaps the simplest example of a scalar field is a weather map showing temperature spots around the country. A more complex example: how the universe is divided into fields: portions of space that have certain characteristics. The image below shows how each point in space can be given a number (in this case, for the temperature of that exact point). Here, the intensity of the scalar field is shown by changing color hues:
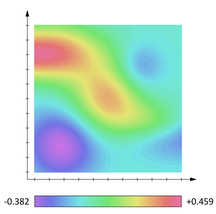
Scalar fields can (and often must) have units associated with them, but they must be independent of the reference frame; Two different observers, using the same system of measurement, should be able to map the same field in exactly the same way.
Other examples of scalar fields: the pressure distribution in a fluid and the electric potential in electrostatics. In scalar theories of gravitation, scalar fields are used to describe the gravitational field.
Representations of Scalar Fields
There are a number of different ways that we can use to represent scalar fields. Sometimes we just have an equation, mapping three dimensions into one, that tells us what scalar goes with every single point in space. This is the most concise way of representing a scalar field, but it is not the most visually intuitive.
Sometimes we fix one of the independent variables and show a contour map for the two remaining dimensions. The curves in this contour map will represent lines of constant values of the function. The downside of this is that you’ll need a series of maps (for different fixed values of z) to get a good feel for the properties of your scalar field.
Color coding, as in the image above, is perhaps a better way to represent the scalar field. It is important the colors are well defined.
A final way of representing fields is with a relief map, where again one of the dimensions are fixed and then the value of the function is plotted as height versus the other two spatial coordinates. The result of this looks like a topographic relief map.
5. Scalar and Scalar Multiples in Linear Algebra
Scalars are used in matrix multiplication. When a matrix is multiplied by a number (a scalar), each element in the matrix is multiplied by that number to create a new matrix. In the following image, the matrix {9,3; 5,7} is multiplied by the scalar 2. The new matrix is called a scalar multiple. In this case, it’s a scalar multiple of 2.

6. Can a Scalar be Negative?
A number like -10 can be a scalar or a vector depending on what situation you are using it in. In linear algebra, scalars can be negative. A negative scalar like -10 would result in a vector in the opposite direction. In physics, scalars and vectors are defined by what happens to them during rotations. Direction is sometimes denoted with a + or – to mean the positive or negative direction relative to a reference point. In this situation, -10 would not be a vector as -10 would mean 10 units in the negative direction from the reference point. To avoid confusion, the word “scalar” in physics is sometimes limited to complex numbers.
References
Arfken, G. (1985). Vector Analysis. Ch. 1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 1-84.
Aris, R. (1985). Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, 1989.
Crowe, M. J. A History of Vector Analysis: The Evolution of the Idea of a Vectorial System. New York: Dover.
Duffy, A. Motion in One Dimension. Retrieved March 30, 2019 from:http://physics.bu.edu/~duffy/py105/Motion1D.html
Hirschfield, P. J. Phz 3113 Class Notes. Retrieved from http://www.phys.ufl.edu/~pjh/teaching/phz3113/notes/week5.pdf on Aug 3, 2019.
MIT TEAL/ Studio Physics Project. Physics 8.02 Electricity and Magnetism. Fields. Retrieved from http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/coursenotes/modules/guide01.pdf on Aug 3, 2019
Scalar Valued Functions. MIT World Web Math. Retrieved from http://web.mit.edu/wwmath/vectorc/scalar/intro.html on May 15, 2019
Venkataraman, P. Scalar Fields in Fluid Mechanics. Retrieved from https://people.rit.edu/pnveme/personal/pigf/Vectors/vec_scalarfld_1.html on May 15, 2019
Comprehensive Physics XI. Laxmi Publications.