Volume of Cone Proof using Calculus (Click to skip to that section):
- Volume Overview
- Volume of a Cube (with Integration)
- Volume of Cone (Proof)
- Volume of an Egg
- Washer Method (Opens in New Window)
1. Volume Calculus: Overview
Volume is the amount of space that some shape occupies in 3D space. One of the best ways to think about it is to relate it to the amount of water an object can contain. This means that the capacity of the shape is actually the volume of it. Volume can be measured in many units, but the standard one is in cubic meters (m3).
One-dimensional figures and two-dimensional shapes have no volume. This means that in lines, triangles, circles and squares have zero capacity. In other words, the concept of volume only works in three dimensions.
When dealing with simple shapes (like platonic solids), you could calculate volume with the help of fairly simple formulas. However, if you’re dealing with complicated forms, then it will be solved by using integral calculus.
Finding Volume

If we wanted to calculate the size of this shape without using calculus, we just need to multiply its length, width, and height.
- The length is the longest side on either the top or the bottom of the prism. In this case, it would be ‘a.’
- After this, we check the shorter side on the top or bottom, in this case, ‘b.’ These two sides form a rectangle, and we need the height to make it three dimensional.
- Finally, ‘c’ is the height as it stretches up from the flat surface created by ‘a’ and ‘b.’
After this, multiply all the sides together in any order, example: a * b * c. When we assign values to them, example: a = 5, b = 4, c = 3, then the volume of the shape will be:
a * b * c = 5 * 4 * 3 = 60 units squared.
Since we’re working in 3D space, it is essential to add the unit in which you’re working, squared.
2. Volume of a Cube with Calculus
To solve a cube with integrals, use this formula. The variable ‘x’ is the length of a side: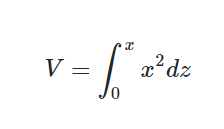
How to solve: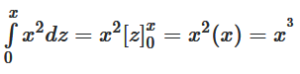
Let’s say that we are solving for a cube that has a side of 3 units.
- Put 3 in the place of ‘x’ since that is the length of all the sides. Now, the integral will have bounds that go from ‘0’ to ‘3’.
- After we solve it, we will get 32 multiplied by ‘z’ in the same bounds.
The result: 32 * 3 = 27 units cubed. - You will get to the same result if you multiply all the sides together, as a backup, to know that you solved it correctly.
3. Volume of Cone Proof
The volume V of a cone, with a height H and a base radius R, is given by the formula V = πR2H⁄3. For example, if we had a cone that has a height of 4 inches and a radius of 2 inches, its volume would be V = π (2)2 (4)⁄3 = 16π⁄3, which is about 16.76 cubic inches. The formula can be proved using integration. Like most proofs, there’s more than one approach. Below you’ll find two examples of how to prove the volume of a cone; They approach the proof in slightly different ways.
How to prove the volume of a cone using integration: Example 1
Example problem: Prove the volume of a cone with h = 4 and r = 2 using calculus.
Step 1: Imagine slicing the cone into very thin circular disks parallel to its circular base.
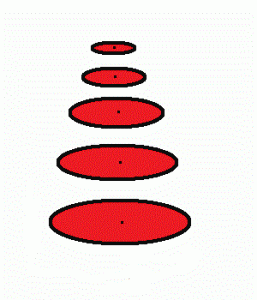
Step 2: Calculate the volume of each disk. Each disk has an infinitesimal thickness, dh (use “dh” to indicate that it is a very, very small “height”). Each of these disks also has a circular area A = πr2, where r is the radius, and disk volume dV = πr2dh, which is the product of the area and the thickness. In the sample cone given above, the variable r ranges from 0 to 2 inches while h goes from 0 at the base to 4 inches at the cone’s tip.
Step 3: Relate each disk’s position to its radius. The disk radius r is related to the disk’s distance h from the base of the cone. This relationship is defined by the line that traces the inclined surface of the cone from its sharp tip to the edge of its circular base, and is given by the linear equation h = (-H⁄R) r + H. Recall that any line follows the form y = mx + b, where y is the vertical coordinate, m is the slope of the line, x is the horizontal coordinate and b is the value of y when the line crosses the y-axis. Therefore, you can replace y with h, x with r, m with -H⁄R, and b with H. For the cone in our example, we have:
h = (-4⁄2) r + 4 = -2r + 4.
Step 4: Add the volumes of the thin disks. To get the total volume of the cone, integrate the volumes of all the tiny disks from the base of the cone to its tip:
V = ∫dV = ∫ πr2dh, where the range of integration over the cone’s height h is from 0 to H.
From the linear relationship of h and r given above, replace r by (R – Rh⁄H):
V = ∫ π(R – Rh⁄H)2dh = πR2 ∫ (1 – h⁄H)2 dh = πR2 ∫ (1 – 2h⁄H + h2⁄H2) dh = πR2 (H – H + H/3) = πR2H⁄3.
For our sample cone, the integration is done over the range 0 ≤ h ≤ 4.
That’s how to prove the volume of a cone with calculus!
Tip: The equation in Step 3 is easy to visualize if you define a coordinate system where the y-axis goes from the center of the circular base up to the sharp tip of the cone and the x-axis goes from the center of the base to its edge. Also, if you have difficulty following the integration in Step 4, recall that ∫ chn dh = (h(n + 1))⁄(n + 1).
How to prove the volume of a cone using integration: Example 2
Calculus can be used to figure the incremental radii of the “slices” and solve for the volume. This next example specifically uses u substitution to solve the integrals.
Steps
Step 1: Find the radius of the base of the cone, which can be found by dividing the diameter of the base by 2. Label this quantity R. Label the height of the cone h.
Step 2: Using the equations for the geometry of a triangle and a circle, set up an equation for the area of each of the circles at an unknown height of x. Visualize the cone as if it were cut down the center, resulting in a flat triangular surface. Using that visualization, you can see how a triangle relates to the area of the cone. This equation is:
A(x) = π * (R2 / h2) * (h – x)2.
The integral equation for the volume of a cone is:
Vcone = ![]() A(x)dx.
A(x)dx.
Step 3: Substituting the previous equation of
A(x) = π * (R2/h2) * (h – x)2 into the integral equation results in the equation:
Vcone = ![]() π*(R2/h2)*(h-x)2*dx, which simplifies to:
π*(R2/h2)*(h-x)2*dx, which simplifies to:
π*(R2/h2) ![]() (h – x)2*dx.
(h – x)2*dx.
Step 4: Use u-substitution to replace h – x with du, so that du = -dx.
The new integral is π*(R2/h2)*(-![]() u2*du.
u2*du.
Step 5: Simplifying this integral results in the equation Vcone = 1/3*π*R2*h, which then can in turn be solved for the volume of the cone.
That’s how to prove the volume of a cone with calculus!
Volume of an Egg
Although this is a step by step guide to how to find the volume of an egg using calculus, you should be familiar with basic integration before working through the steps.
How to Find the Volume of an Egg using Calculus: Steps
Step 1: Draw the egg using an ellipse and sphere and make sure that they overlap each other. Split the egg into two parts by drawing a line over the vertical axis of the ellipse and draw another horizontal line that splits the egg into two equal parts. These are your X and Y axes.
Step 2: Name the points where the egg intersects the two axis as follows: (0, n ) and (0, -n ) on the vertical line and (-m, 0) and (m, 0) on the horizontal one.
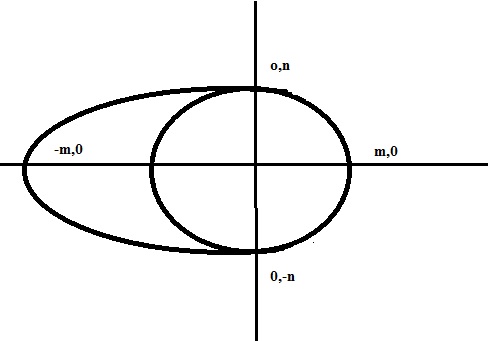
Step 3: Split your egg into 2 parts. Have the left part of the ellipse in one half and the circle in the other. Remove anything below the horizontal line and you should now have two drawings, one with the upper left part of an ellipse and the other with the upper right part of the circle.
Step 4: Calculate the circle’s area and use the volume by revolution formula which rotates the circle along the X axis resulting in volume.
This is the equation: Integrate π (n2-X2) from 0 to n.
You can use this online integrator to help you.
Step 5 : Calculate the circle integral and factorize π:
π [∫(n2-X2)] from [0 to n]
Solve the integral by using the online integrator.
Replace 0 and n and you should get
π [((n2 * n) – (n3/3)) – ((n2 * 0) – (03/3))]
resulting ( 2/3 ) π * n3.
Step 6: Find the volume of the ellipse. Do this by integrating π( (n2/m2) (m2-X2) ) from [-m to 0 ].
Step 7: Solve the integral of the ellipse, and factorize π:
π * ∫ ((n2/m2)*(m2-X2)) from [-m to 0]
Use the Online Integrator again.
You will get:
π * [(1/3)(n2)(X)(3-(X2/m2)] from [-m to 0]
After replacing -m and 0 and doing the simplifications your result will be (2/3) π * n2 * m.
Step 8: Get the total volume of the egg by summing up half the volume of the sphere with half the volume of the ellipse. After simplification the answer is (2/3) π * n2 * (m+n).
Step 9: Replace m and n with numbers in the (2/3) π * n2 * (m+n) equation and your result should be around 1.8 cubic inches, more or less depending on the size of the egg.
Here is an example:
An average chicken egg is 5.6 cm long and has a diameter of 4.4 cm at its widest part. Now let’s replace m and n with the proper numbers in the last formula.
Diameter is 4.4 so n= 2.2 cm
Length is m + 2.2 = 5.6 so m= 3.4
(2/3) π * 2.22 * (2.2 + 3.4 ) = 28,368 cubic centimeters which is almost 2 cubic inches, 1.73 to be more precise.
That’s How to Find the Volume of an Egg !