A unit square has one unit for each side. The unit is problem specific. For example, if you’re working with cm, the unit square would have sides of 1 cm and would contain one square cm—an area of 1 cm2.
Sometimes we refer to “the” unit square in mathematics. Most of that time, that means a unit square positioned so that the bottom left of the square is at the origin (0, 0) in the Cartesian plane.
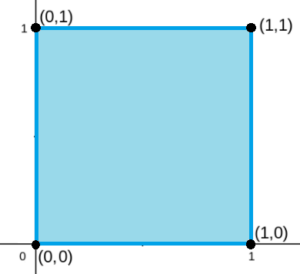
One way to define it is as a square where points x and y lie in a closed unit interval [0, 1]. The closed unit interval is sometimes denoted as the symbol I.
You can graph the unit square with the equation |x – y| + |x + y – 1| = 1. For example, here’s the square graphed on Desmos. In the complex plane, it is found at coordinates 0, 1, 1 + i, and i.
“Over the Unit Square”
“Over the unit square” means, generally, that the problem you’re looking at is contained within the boundaries of (0,1) (0, 1), (1, 1), (1, 0). For example, in probability, a joint distribution that is “over the unit square” consists of a set of points with x and y coordinates between 0 and 1.
Cardinality
A unit square [0, 1] x [0, 1] can be mapped one-to-one to the unit interval [0, 1]; They have the same cardinality even though they have different dimensions, a proof of which was outlined by Georg Cantor (Bradley, 2006).
References
Blumel, R. (2011). Advanced Quantum Mechanics. The Classical-Quantum Connection. Jones & Bartlett Learning.
Bradley, M. (2006). The Foundations of Mathematics: 1800 to 1900. Facts on File, Incorporated.
Guy, R. (1991). Unsolved Problems in Number Theory, Vol. 1 (2nd ed.), Springer-Verlag, pp. 181–185
Hadwiger, H. & Debrunner, H. (1964). Combinatorial Geometry in the Plane. Translated by V. Klee. With a new chapter and additional material supplied by the translator. Holt, Rinehart and Winston, New York.
Katz, R. et al. (n.d.). Zero Sums on US Vertex Sets and Plane Colorings. Retrieved October 21, 2020 from: https://www.calstatela.edu/sites/default/files/users/u2536/ResearchFiles/amer.math_.monthly.121.07.610-krebs.pdf
Manshad, A. Square and Cubic Units. Retrieved October 21, 2020 from: https://web.nmsu.edu/~pbaggett/Lessons/SACU/SACU.html